
设函数![]() ,已知关于
,已知关于![]() 的方程
的方程![]() 的两个根为
的两个根为![]() ,
,
(1)判断![]() 在
在![]() 上的单调性;
上的单调性;
(2)若![]() ,证明
,证明![]() .
.
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:
设某物体一天中的温度T是时间t的函数,已知![]() ,其中温度的单位是℃,时间的单位是小时.中午12:00相应的t=0,中午12:00以后相应的t取正数,中午12:00以前相应的t取负数(如早上8:00相应的t=-4,下午16:00相应的t=4).若测得该物体在早上8:00的温度为8℃,中午12:00的温度为60℃,下午13:00的温度为58℃,且已知该物体的温度早上8:00与下午16:00有相同的变化率.
,其中温度的单位是℃,时间的单位是小时.中午12:00相应的t=0,中午12:00以后相应的t取正数,中午12:00以前相应的t取负数(如早上8:00相应的t=-4,下午16:00相应的t=4).若测得该物体在早上8:00的温度为8℃,中午12:00的温度为60℃,下午13:00的温度为58℃,且已知该物体的温度早上8:00与下午16:00有相同的变化率.
(1)求该物体的温度T关于时间t的函数关系式;
(2)该物体在上午10:00到下午14:00这段时间中(包括端点)何时温度最高?最高温度是多少?
查看答案和解析>>
科目:高中数学 来源:2010年浙江省杭州市严州中学高考数学模拟试卷(理科)(解析版) 题型:解答题
 ,已知
,已知 时f(x)取到最大值2.
时f(x)取到最大值2. 对称,求满足x∈(0,π)且f(x)-2g(x)=3的所有x的值.
对称,求满足x∈(0,π)且f(x)-2g(x)=3的所有x的值.查看答案和解析>>
科目:高中数学 来源:2010-2011学年山东省高三第一次质量检测理科数学卷 题型:解答题
(满分12分)
设某物体一天中的温度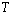 是时间
是时间 的函数,已知
的函数,已知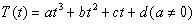 ,其中温度的单位是℃,时间的单位是小时.中午12:00相应的
,其中温度的单位是℃,时间的单位是小时.中午12:00相应的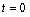 ,中午12:00以后相应的
,中午12:00以后相应的 取正数,中午12:00以前相应的
取正数,中午12:00以前相应的 取负数(如早上8:00相应的t=-4,下午16:00相应的t=4).若测得该物体在早上8:00的温度为8℃,中午12:00的温度为60℃,下午13:00的温度为58℃,且已知该物体的温度早上8:00与下午16:00有相同的变化率.
取负数(如早上8:00相应的t=-4,下午16:00相应的t=4).若测得该物体在早上8:00的温度为8℃,中午12:00的温度为60℃,下午13:00的温度为58℃,且已知该物体的温度早上8:00与下午16:00有相同的变化率.
(I)求该物体的温度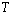 关于时间
关于时间 的函数关系式;
的函数关系式;
(II)该物体在上午10:00到下午14:00这段时间中(包括端点)何时温度最高?最高温度是多少?
查看答案和解析>>
科目:高中数学 来源:2010-2011学年山东省高三第一次质量检测理科数学卷 题型:解答题
(满分12分)
设某物体一天中的温度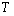 是时间
是时间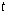 的函数,已知
的函数,已知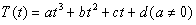 ,其中温度的单位是℃,时间的单位是小时.中午12:00相应的
,其中温度的单位是℃,时间的单位是小时.中午12:00相应的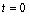 ,中午12:00以后相应的
,中午12:00以后相应的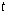 取正数,中午12:00以前相应的
取正数,中午12:00以前相应的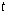 取负数(如早上8:00相应的t=-4,下午16:00相应的t=4).若测得该物体在早上8:00的温度为8℃,中午12:00的温度为60℃,下午13:00的温度为58℃,且已知该物体的温度早上8:00与下午16:00有相同的变化率.
取负数(如早上8:00相应的t=-4,下午16:00相应的t=4).若测得该物体在早上8:00的温度为8℃,中午12:00的温度为60℃,下午13:00的温度为58℃,且已知该物体的温度早上8:00与下午16:00有相同的变化率.
(I)求该物体的温度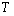 关于时间
关于时间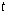 的函数关系式;
的函数关系式;
(II)该物体在上午10:00到下午14:00这段时间中(包括端点)何时温度最高?最高温度是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com