
【题目】在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,M是侧棱
,M是侧棱![]() 上一点,设
上一点,设![]() .
.
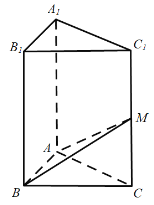
(1)若![]() ,求多面体
,求多面体![]() 的体积;
的体积;
(2)若异面直线BM与![]() 所成的角为
所成的角为![]() ,求h的值.
,求h的值.
【答案】(1)![]() ;(2)2
;(2)2
【解析】
(1)多面体![]() 的体积为
的体积为![]() ,由此能求出结果;
,由此能求出结果;
(2)以B为原点,BC为x轴,BA为y轴,BB1为z轴,建立空间直角坐标系,利用向量法能求出h的值.
解:(1)∵在直三棱柱ABC﹣A1B1C1中,AB⊥BC,AB=BC=2,
![]() ,M是侧棱C1C上一点,设MC=
,M是侧棱C1C上一点,设MC=![]() ,
,
∴多面体ABM﹣A1B1C1的体积为:
![]()
=![]() ﹣
﹣![]()
=![]()
=![]() .
.
(2)以B为原点,BC为x轴,BA为y轴,BB1为z轴,建立空间直角坐标系,
则B(0,0,0),M(2,0,h),A1(0,2,2![]() ),C1(2,0,2
),C1(2,0,2![]() ),
),
![]() =(2,0,h),
=(2,0,h),![]() =(2,﹣2,0),
=(2,﹣2,0),
∵异面直线BM与A1C1所成的角为60°,
∴cos60°=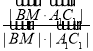 =
=![]() ,
,
由h>0,解得h=2.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:
【题目】中国在欧洲的某孔子学院为了让更多的人了解中国传统文化,在当地举办了一场由当地人参加的中国传统文化知识大赛,为了了解参加本次大赛参赛人员的成绩情况,从参赛的人员中随机抽取![]() 名人员的成绩(满分100分)作为样本,将所得数据进行分析整理后画出频率分布直方图如图所示,已知抽取的人员中成绩在[50,60)内的频数为3.
名人员的成绩(满分100分)作为样本,将所得数据进行分析整理后画出频率分布直方图如图所示,已知抽取的人员中成绩在[50,60)内的频数为3.
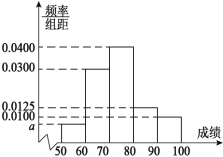
(1)求![]() 的值和估计参赛人员的平均成绩(保留小数点后两位有效数字);
的值和估计参赛人员的平均成绩(保留小数点后两位有效数字);
(2)已知抽取的![]() 名参赛人员中,成绩在[80,90)和[90,100]女士人数都为2人,现从成绩在[80,90)和[90,100]的抽取的人员中各随机抽取2人,记这4人中女士的人数为
名参赛人员中,成绩在[80,90)和[90,100]女士人数都为2人,现从成绩在[80,90)和[90,100]的抽取的人员中各随机抽取2人,记这4人中女士的人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() (其中
(其中![]() ,点P的轨迹记为曲线
,点P的轨迹记为曲线![]() ,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点Q在曲线
,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点Q在曲线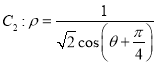 上.
上.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)当![]() ,
,![]() 时,求曲线
时,求曲线![]() 与曲线
与曲线![]() 的公共点的极坐标
的公共点的极坐标
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() :
:![]() 的离心率
的离心率![]() ,其左焦点
,其左焦点![]() 到此双曲线渐近线的距离为
到此双曲线渐近线的距离为![]() .
.
(1)求双曲线![]() 的方程;
的方程;
(2)若过点![]() 的直线
的直线![]() 交双曲线
交双曲线![]() 于
于![]() 两点,且以
两点,且以![]() 为直径的圆
为直径的圆![]() 过原点
过原点![]() ,求圆
,求圆![]() 的圆心到抛物线
的圆心到抛物线![]() 的准线的距离.
的准线的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 由方程
由方程![]() 确定,对于函数
确定,对于函数![]() 给出下列命题:
给出下列命题:
①存在![]() ,
,![]() ,使得
,使得![]() 成立;
成立;
②![]() ,
,![]() ,使得
,使得![]() 且
且![]() 同时成立;
同时成立;
③对于任意![]() ,
,![]() 恒成立;
恒成立;
④对任意![]() ,
,![]() ,
,![]() ;都有
;都有![]() 恒成立.
恒成立.
其中正确的命题共有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十项全能是由跑、跳、投等10个田径项目组成的综合性男子比赛项目,按照国际田径联合会制定的田径运动全能评分表计分,然后将各个单项的得分相加,总分多者为优胜.下面是某次全能比赛中甲、乙两名运动员的各个单项得分的雷达图.
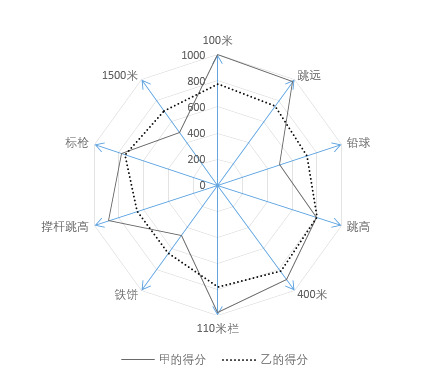
下列说法错误的是( )
A.在100米项目中,甲的得分比乙高
B.在跳高和标枪项目中,甲、乙的得分基本相同
C.甲的各项得分比乙更均衡
D.甲的总分高于乙的总分
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com