
【题目】离心率为![]() 的椭圆
的椭圆![]() 经过点
经过点![]() ,
,![]() 是坐标原点.
是坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆![]() 恒有两个交点
恒有两个交点![]() ,且
,且![]() ?若存在,求出该圆的方程,并求
?若存在,求出该圆的方程,并求![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】(1)![]() ;
;
(2)存在,理由见解析;圆的方程为![]() ;
;![]() .
.
【解析】
(1)利用离心率和椭圆所过点联立方程组可求椭圆的方程;
(2)先假设存在符合要求的圆,利用![]() 求出圆的切线,结合弦长公式表示出
求出圆的切线,结合弦长公式表示出![]() ,利用基本不等式求解范围.
,利用基本不等式求解范围.
(1)因为椭圆![]() 经过点
经过点![]() ,所以
,所以![]() ;
;
又离心率为![]() ,所以
,所以![]() ,结合
,结合![]() 可得
可得![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)假设存在圆心在原点的圆,使得该圆的任意一条切线与椭圆![]() 恒有两个交点
恒有两个交点![]() ,且
,且![]() ,设圆的切线方程为
,设圆的切线方程为![]() ,
,![]() .
.
联立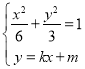 得
得![]() ,
,
![]()
即![]() .
.
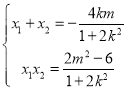
![]()
因为![]() ,所以
,所以![]() ,即
,即![]() ,
,
所以![]() ,即
,即![]() ;
;
因为圆的切线方程为![]() ,所以圆的半径为
,所以圆的半径为![]() ,
,![]() ,所求圆的方程为
,所求圆的方程为![]() .
.
由![]() 及
及![]() 可得
可得![]() ,即
,即![]() 或
或![]() ;
;
当圆的切线斜率不存在时,切线方程为![]() ,切线与椭圆的交点为
,切线与椭圆的交点为![]() 或者
或者![]() ,均满足
,均满足![]() .
.
综上可知,存在圆心在原点的圆,使得该圆的任意一条切线与椭圆![]() 恒有两个交点
恒有两个交点![]() ,且
,且![]() .
.
因为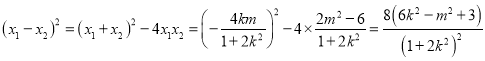
所以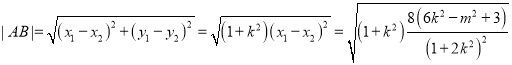
![]()
当![]() 时,由于
时,由于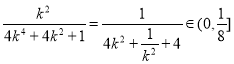 ,所以
,所以![]() ,当且仅当
,当且仅当![]() 时,取到最大值3;
时,取到最大值3;
当![]() 时,
时,![]() ;
;
当斜率不存在时,直线![]() 与椭圆交于
与椭圆交于![]() 或者
或者![]() 此时
此时![]() .
.
综上可知,![]() .
.


科目:高中数学 来源: 题型:
【题目】近年来,随着我国汽车消费水平的提高,二手车流通行业得到迅猛发展.某汽车交易市场对2017年成交的二手车交易前的使用时间(以下简称“使用时间”)进行统计,得到频率分布直方图如图1.


图1 图2
(1)记“在![]() 年成交的二手车中随机选取一辆,该车的使用年限在
年成交的二手车中随机选取一辆,该车的使用年限在![]() ”为事件
”为事件![]() ,试估计
,试估计![]() 的概率;
的概率;
(2)根据该汽车交易市场的历史资料,得到散点图如图2,其中![]() (单位:年)表示二手车的使用时间,
(单位:年)表示二手车的使用时间,![]() (单位:万元)表示相应的二手车的平均交易价格.由散点图看出,可采用
(单位:万元)表示相应的二手车的平均交易价格.由散点图看出,可采用![]() 作为二手车平均交易价格
作为二手车平均交易价格![]() 关于其使用年限
关于其使用年限![]() 的回归方程,相关数据如下表(表中
的回归方程,相关数据如下表(表中![]() ,
,![]() ):
):

①根据回归方程类型及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
②该汽车交易市场对使用8年以内(含8年)的二手车收取成交价格![]() 的佣金,对使用时间8年以上(不含8年)的二手车收取成交价格
的佣金,对使用时间8年以上(不含8年)的二手车收取成交价格![]() 的佣金.在图1对使用时间的分组中,以各组的区间中点值代表该组的各个值.若以2017年的数据作为决策依据,计算该汽车交易市场对成交的每辆车收取的平均佣金.
的佣金.在图1对使用时间的分组中,以各组的区间中点值代表该组的各个值.若以2017年的数据作为决策依据,计算该汽车交易市场对成交的每辆车收取的平均佣金.
附注:①对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ;
;
②参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我区的中小学办学条件在政府的教育督导下,迅速得到改变.督导一年后.分别随机抽查了高中(用![]() 表示)与初中(用
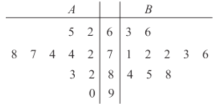
表示)与初中(用![]() 表示)各10所学校.得到相关指标的综合评价得分(百分制)的茎叶图如图所示.则从茎叶图可得出正确的信息为(80分及以上为优秀)( )
表示)各10所学校.得到相关指标的综合评价得分(百分制)的茎叶图如图所示.则从茎叶图可得出正确的信息为(80分及以上为优秀)( )
①高中得分与初中得分的优秀率相同
②高中得分与初中得分的中位数相同
③高中得分的方差比初中得分的方差大
④高中得分与初中得分的平均分相同
A.①②B.①③C.②④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
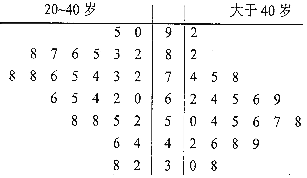
【题目】某公司即将推车一款新型智能手机,为了更好地对产品进行宣传,需预估市民购买该款手机是否与年龄有关,现随机抽取了50名市民进行购买意愿的问卷调查,若得分低于60分,说明购买意愿弱;若得分不低于60分,说明购买意愿强,调查结果用茎叶图表示如图所示.
(1)根据茎叶图中的数据完成![]() 列联表,并判断是否有95%的把握认为市民是否购买该款手机与年龄有关?
列联表,并判断是否有95%的把握认为市民是否购买该款手机与年龄有关?
购买意愿强 | 购买意愿弱 | 合计 | |
20-40岁 | |||
大于40岁 | |||
合计 |
(2)从购买意愿弱的市民中按年龄进行分层抽样,共抽取5人,从这5人中随机抽取2人进行采访,记抽到的2人中年龄大于40岁的市民人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附: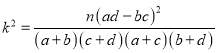 .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一款击鼓小游戏的规则如下:每盘游戏都需击鼓三次,每次击鼓后要么出现一次音乐,要么不出现音乐;每盘游戏击鼓三次后,出现三次音乐获得150分,出现两次音乐获得100分,出现一次音乐获得50分,没有出现音乐则获得-300分.设每次击鼓出现音乐的概率为![]() ,且各次击鼓出现音乐相互独立.
,且各次击鼓出现音乐相互独立.
(1)若一盘游戏中仅出现一次音乐的概率为![]() ,求
,求![]() 的最大值点
的最大值点![]() ;
;
(2)以(1)中确定的![]() 作为
作为![]() 的值,玩3盘游戏,出现音乐的盘数为随机变量
的值,玩3盘游戏,出现音乐的盘数为随机变量![]() ,求每盘游戏出现音乐的概率
,求每盘游戏出现音乐的概率![]() ,及随机变量
,及随机变量![]() 的期望
的期望![]() ;
;
(3)玩过这款游戏的许多人都发现,若干盘游戏后,与最初的分数相比,分数没有增加反而减少了.请运用概率统计的相关知识分析分数减少的原因.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x﹣a|+|x![]() |(a>0).
|(a>0).
(1)若不等式f(x)﹣| x![]() |≥4x的解集为{x|x≤1},求实数a的值;
|≥4x的解集为{x|x≤1},求实数a的值;
(2)证明:f(x)![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com