
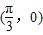 中心对称,那么|φ|的最小值为( )
中心对称,那么|φ|的最小值为( )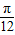
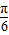
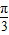
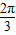
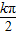 ,0),可得y=5tan(2x+φ)的对称中心,又函数y=5tan(2x+φ)的图象关于点
,0),可得y=5tan(2x+φ)的对称中心,又函数y=5tan(2x+φ)的图象关于点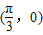 中心对称,从而可得到φ的关系式,验证即可.
中心对称,从而可得到φ的关系式,验证即可.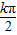 ,0),
,0),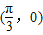 中心对称,
中心对称,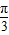 +φ=
+φ=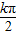 ,
,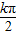 -
-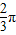 ,
,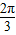 ;k=1时,φ=-
;k=1时,φ=-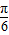 ;k=2时,φ=
;k=2时,φ=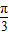 ,k=3时,φ=
,k=3时,φ=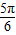 ,…
,…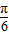 .
.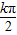 ,0),正切函数y=tanωx的对称中心受ω的影响,难点在于对“2•
,0),正切函数y=tanωx的对称中心受ω的影响,难点在于对“2•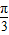 +φ=
+φ=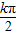 ”的理解与应用,属于中档题.
”的理解与应用,属于中档题. 

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com