
【题目】已知函数![]() .
.
(1)讨论![]() 极值点的个数;
极值点的个数;
(2)若![]() 是
是![]() 的一个极值点,且
的一个极值点,且![]() ,证明:
,证明: ![]() .
.
【答案】(1) 当![]() 时,
时,![]() 无极值点;当
无极值点;当![]() 时,
时,![]() 有
有![]() 个极值点;当
个极值点;当![]() 或
或![]() 时,
时,![]() 有
有![]() 个极值点;(2)证明见解析
个极值点;(2)证明见解析
【解析】
(1)求导得到![]() ;分别在
;分别在![]() 、
、![]() 、
、![]() 和
和![]() 四种情况下根据
四种情况下根据![]() 的符号确定
的符号确定![]() 的单调性,根据极值点定义得到每种情况下极值点的个数;(2)由(1)的结论和
的单调性,根据极值点定义得到每种情况下极值点的个数;(2)由(1)的结论和![]() 可求得
可求得![]() ,从而得到
,从而得到![]() ,代入函数解析式可得
,代入函数解析式可得![]() ;令
;令![]() 可将
可将![]() 化为关于
化为关于![]() 的函数
的函数![]() ,利用导数可求得
,利用导数可求得![]() 的单调性,从而得到
的单调性,从而得到![]() ,进而得到结论.
,进而得到结论.
(1)![]()
①当![]() 时,
时,![]()
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
![]() 在
在![]() 上单调递减;在
上单调递减;在![]() 上单调递增
上单调递增
![]() 为
为![]() 的唯一极小值点,无极大值点,即此时
的唯一极小值点,无极大值点,即此时![]() 极值点个数为:
极值点个数为:![]() 个
个
②当![]() 时,令
时,令![]() ,解得:
,解得:![]() ,
,![]()
⑴当![]() 时,
时,![]()
![]() 和
和![]() 时,
时,![]() ;
;![]() 时,
时,![]()
![]() 在
在![]() ,
,![]() 上单调递增;在
上单调递增;在![]() 上单调递减
上单调递减
![]() 为
为![]() 的极大值点,
的极大值点,![]() 为
为![]() 的极小值点,即
的极小值点,即![]() 极值点个数为:
极值点个数为:![]() 个
个
⑵当![]() 时,
时,![]() ,此时
,此时![]() 恒成立且不恒为
恒成立且不恒为![]()
![]() 在
在![]() 上单调递增,无极值点,即
上单调递增,无极值点,即![]() 极值点个数为:
极值点个数为:![]() 个
个
⑶当![]() 时,
时,![]()
![]() 和
和![]() 时,
时,![]() ;
;![]() 时,
时,![]()
![]() 在
在![]() ,
,![]() 上单调递增;在
上单调递增;在![]() 上单调递减
上单调递减
![]() 为
为![]() 的极大值点,
的极大值点,![]() 为
为![]() 的极小值点,即
的极小值点,即![]() 极值点个数为:
极值点个数为:![]() 个
个
综上所述:当![]() 时,
时,![]() 无极值点;当
无极值点;当![]() 时,
时,![]() 有
有![]() 个极值点;当
个极值点;当![]() 或
或![]() 时,
时,![]() 有
有![]() 个极值点
个极值点
(2)由(1)知,若![]() 是
是![]() 的一个极值点,则
的一个极值点,则![]()
又![]() ,即
,即![]()
![]()
![]()
![]()
![]() 令
令![]() ,则
,则![]()
![]() ,
,![]()
则![]()
当![]() 时,
时,![]() ,
,![]()
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
![]() 在
在![]() 上单调递增;在
上单调递增;在![]() 上单调递减
上单调递减
![]() ,即
,即![]()
![]()


 优等生题库系列答案
优等生题库系列答案科目:高中数学 来源: 题型:
【题目】如果数列![]() 对于任意
对于任意![]() ,都有
,都有![]() ,其中
,其中![]() 为常数,则称数列
为常数,则称数列![]() 是“间等差数列”,
是“间等差数列”,![]() 为“间公差”.若数列
为“间公差”.若数列![]() 满足
满足![]() ,
,![]() ,
,![]() .
.
(1)求证:数列![]() 是“间等差数列”,并求间公差
是“间等差数列”,并求间公差![]() ;
;
(2)设![]() 为数列
为数列![]() 的前n项和,若
的前n项和,若![]() 的最小值为-153,求实数
的最小值为-153,求实数![]() 的取值范围;
的取值范围;
(3)类似地:非零数列![]() 对于任意
对于任意![]() ,都有
,都有![]() ,其中
,其中![]() 为常数,则称数列
为常数,则称数列![]() 是“间等比数列”,
是“间等比数列”,![]() 为“间公比”.已知数列
为“间公比”.已知数列![]() 中,满足
中,满足![]() ,
,![]() ,
,![]() ,试问数列
,试问数列![]() 是否为“间等比数列”,若是,求最大的整数
是否为“间等比数列”,若是,求最大的整数![]() 使得对于任意
使得对于任意![]() ,都有
,都有![]() ;若不是,说明理由.
;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场营销人员进行某商品M市场营销调查发现,每回馈消费者一定的点数,该商品每天的销量就会发生一定的变化,经过试点统计得到以下表:
反馈点数 | 1 | 2 | 3 | 4 | 5 |
销量(百件)/天 | 0. 5 | 0. 6 | 1 | 1. 4 | 1. 7 |
(1)经分析发现,可用线性回归模型拟合当地该商品销量![]() (百件)与返还点数
(百件)与返还点数![]() 之间的相关关系. 请用最小二乘法求
之间的相关关系. 请用最小二乘法求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测若返回6个点时该商品每天销量;
,并预测若返回6个点时该商品每天销量;
(2)若节日期间营销部对商品进行新一轮调整. 已知某地拟购买该商品的消费群体十分庞大,经营销调研机构对其中的200名消费者的返点数额的心理预期值进行了一个抽样调查,得到如下一份频数表:
返还点数预期值区间(百分比) |
|
|
|
|
|
|
频数 | 20 | 60 | 60 | 30 | 20 | 10 |
(ⅰ)求这200位拟购买该商品的消费者对返点点数的心理预期值![]() 的样本平均数及中位数的估计值(同一区间的预期值可用该区间的中点值代替;估计值精确到0. 1);
的样本平均数及中位数的估计值(同一区间的预期值可用该区间的中点值代替;估计值精确到0. 1);
(ⅱ)将对返点点数的心理预期值在![]() 和
和![]() 的消费者分别定义为“欲望紧缩型”消费者和“欲望膨胀型”消费者,现采用分层抽样的方法从位于这两个区间的30名消费者中随机抽取6名,再从这6人中随机抽取2名进行跟踪调查,设抽出的2人中,至少有一个人是“欲望膨胀型”消费者的概率是多少?
的消费者分别定义为“欲望紧缩型”消费者和“欲望膨胀型”消费者,现采用分层抽样的方法从位于这两个区间的30名消费者中随机抽取6名,再从这6人中随机抽取2名进行跟踪调查,设抽出的2人中,至少有一个人是“欲望膨胀型”消费者的概率是多少?
参考公式及数据:①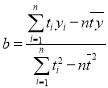 ,
,![]() ;②
;②![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校从参加高一年级期中考试的学生中抽出50名学生,并统计了她们的数学成绩(成绩均为整数且满分为150分),得到的样本频率分布表如下:
分组 | 频数 | 频率 |
| 2 | 0.04 |
| 3 | 0.06 |
| 14 | 0.28 |
| 15 | 0.30 |
|
|
|
| 4 | 0.08 |
合计 |
|
|
(1)在给出的样本频率分布表中,求![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)估计成绩在120分以上(含120分)学生的比例;
(3)抽取的50名学生中,为了帮助成绩差的学生提高数学成绩,学校决定成立“二帮一”小组,即从成绩在![]() 的学生中选两位同学,共同帮助成绩在
的学生中选两位同学,共同帮助成绩在![]() 中的某一位同学.已知甲同学的成绩为62分,乙同学的成绩为135分,求甲、乙两同学恰好被安排在同一小组的概率.
中的某一位同学.已知甲同学的成绩为62分,乙同学的成绩为135分,求甲、乙两同学恰好被安排在同一小组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是二次函数,且f(0)=0,f(x+1)=f(x)+x+1,
(1)求f(x)的表达式;
(2)若f(x)>a在x∈[﹣1,1]恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)设![]() ,求函数
,求函数![]() 的单调增区间;
的单调增区间;
(2)设![]() ,求证:存在唯一的
,求证:存在唯一的![]() ,使得函数
,使得函数![]() 的图象在点
的图象在点![]() 处的切线l与函数
处的切线l与函数![]() 的图象也相切;
的图象也相切;
(3)求证:对任意给定的正数a,总存在正数x,使得不等式![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层。某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元。该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)=![]() 若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
(Ⅰ)求k的值及f(x)的表达式。
(Ⅱ)隔热层修建多厚时,总费用f(x)达到最小,并求最小值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com