
将圆![]() 按向量a=(-1,2)平移后得到⊙O,直线l与⊙O相交于A、B两点,若在⊙O上存在点C,使
按向量a=(-1,2)平移后得到⊙O,直线l与⊙O相交于A、B两点,若在⊙O上存在点C,使 ![]() =λa,求直线l的方程及对应的点C的坐标.
=λa,求直线l的方程及对应的点C的坐标.
直线l的方程为2x-4y+5=0,对应的C点的坐标为(-1,2);或直线l的方程为2x-4y-5=0,对应的C点的坐标为(1,-2).
圆![]() 化为标准方程为
化为标准方程为![]() ,
,
按向量a=(-1,2)平移得⊙O方程为 x2+y2=5.
∵![]() =λa,且|
=λa,且|![]() |=|
|=|![]() |,∴
|,∴![]() ⊥
⊥![]() ,
,![]() ∥a.
∥a.
∴kAB=![]() .设直线l的方程为y=
.设直线l的方程为y=![]() x+m,联立,得
x+m,联立,得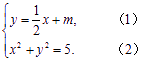
将方程(1)代入(2),整理得5x2+4mx+4m2-20=0.(※)
设A(x1,y1),B(x2,y2),则
x1+x2=-![]() ,y1+y2=
,y1+y2=![]() ,
,![]() =(-
=(-![]() ,
,![]() ).
).
因为点C在圆上,所以![]() ,解之,得
,解之,得![]() .
.
此时,(※)式中的△=16m2-20(4m2-20)=300>0.
所求的直线l的方程为2x-4y+5=0,对应的C点的坐标为(-1,2);或直线l的方程为2x-4y-5=0,对应的C点的坐标为(1,-2).


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
. |
| z1 |
| 1 |
| 2 |
| a |
| 3 |
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源:湖北模拟 题型:单选题
| a |
A.3±
| B.-3±
| C.2±
| D.-2±
|
查看答案和解析>>
科目:高中数学 来源: 题型:
将圆⊙C按向量a=(-1,2)平移后得到⊙O,直线l与⊙O相交于A、B两点,若在⊙O上存在点C,使 ![]() =λa,求直线l的斜率为( )
=λa,求直线l的斜率为( )
A.![]() B.
B.![]() C.-2 D.2
C.-2 D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com