
【题目】上半年产品产量与单位成本资料如下:
月份 | 产量/千件 | 单位成本/元 |
1 | 2 | 73 |
2 | 3 | 72 |
3 | 4 | 71 |
4 | 3 | 73 |
5 | 4 | 69 |
6 | 5 | 68 |
且已知产量x与单位成本y具有线性相关关系.
(1)求出回归方程.
(2)指出产量每增加1 000件时,单位成本平均变动多少?
(3)假定产量为6 000件时,单位成本为多少元?
【答案】(1) ![]() =
=![]() x+
x+![]() =-1.82x+77.37;(2) 1.82元; (3) 大约为66.45元
=-1.82x+77.37;(2) 1.82元; (3) 大约为66.45元
【解析】试题分析:利用一组统计数据求回归直线方程时,需要计算两个变量的的平均数, ![]() 及
及![]() 的和,利用最小二乘法公式求出
的和,利用最小二乘法公式求出![]() ,写出回归直线方程;计算自变量为
,写出回归直线方程;计算自变量为![]() 与子自变量为的预测值
与子自变量为的预测值![]() 的差值,就得到产量每增加1 000件时,单位成本平均变动数;把
的差值,就得到产量每增加1 000件时,单位成本平均变动数;把![]() 代入回归直线方程中,计算可得单位成本y的估计值.
代入回归直线方程中,计算可得单位成本y的估计值.
试题解析:
利用最小二乘法求出回归直线方程,再根据回归方程进行预测.
(1)n=6, ![]() =3.5,
=3.5, ![]() =71,
=71, ![]() =79,
=79, ![]() xiyi=1 481,
xiyi=1 481,
![]() =
=![]() ≈-1.82,
≈-1.82,
![]() =
=![]() -
-![]()
![]()
=71+1.82×3.5=77.37,
则回归方程为![]() =
=![]() x+
x+![]() =-1.82x+77.37.
=-1.82x+77.37.
(2)因为单位成本平均变动![]() =-1.82<0,且产量x的计量单位是千件,所以根据回归系数
=-1.82<0,且产量x的计量单位是千件,所以根据回归系数![]() 的意义有产量每增加一个单位即1 000件时,单位成本平均减少1.82元.
的意义有产量每增加一个单位即1 000件时,单位成本平均减少1.82元.
(3)当产量为6 000件,即x=6时,代入回归方程,
得![]() =77.37-1.82×6=66.45(元).
=77.37-1.82×6=66.45(元).
即当产量为6 000件时,单位成本大约为66.45元.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的离心率为
)的离心率为![]() ,直线
,直线![]() :
: ![]() 与以原点为圆心、椭圆
与以原点为圆心、椭圆![]() 的短半轴长为半径的圆
的短半轴长为半径的圆![]() 相切.
相切.
(1)求椭圆![]() 的方程;
的方程;
(2)过椭圆![]() 的左顶点
的左顶点![]() 作直线
作直线![]() ,与圆
,与圆![]() 相交于两点
相交于两点![]() ,
, ![]() ,若
,若![]() 是钝角三角形,求直线
是钝角三角形,求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,直线![]() 的参数方程为
的参数方程为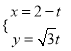 (t为参数),P、Q分别为直线
(t为参数),P、Q分别为直线![]() 与x轴、y轴的交点,线段PQ的中点为M.
与x轴、y轴的交点,线段PQ的中点为M.
(Ⅰ)求直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,求点M的极坐标和直线OM的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市的3个区共有高中学生20 000人,且3个区的高中学生人数之比为2∶3∶5,现要从所有学生中抽取一个容量为200的样本,调查该市高中学生的视力情况,试写出抽样过程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知e为自然对数的底数,设函数![]() ,则( ).
,则( ).
A. 当k=1时,f(x)在x=1处取到极小值 B. 当k=1时,f(x)在x=1处取到极大值
C. 当k=2时,f(x)在x=1处取到极小值 D. 当k=2时,f(x)在x=1处取到极大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,横、纵坐标均为整数的点叫做格点.若函数图象恰好经过k个格点,则称函数为k阶格点函数.已知函数:
①y=sinx; ②y=cos(x+![]() ); ③y=ex-1; ④y=x2.
); ③y=ex-1; ④y=x2.
其中为一阶格点函数的序号为 ( )
A. ①② B. ②③ C. ①③ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人做游戏,下列游戏不公平的是( )
A. 抛掷一枚骰子,向上的点数为奇数则甲获胜,向上的点数为偶数则乙获胜
B. 同时抛掷两枚硬币,恰有一枚正面向上则甲获胜,两枚都正面向上则乙获胜
C. 从一副不含大小王的扑克牌中抽一张,扑克牌是红色的则甲获胜,扑克牌是黑色的则乙获胜
D. 甲、乙两人各写一个数字1或2,如果两人写的数字相同甲获胜,否则乙获胜
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代名词“刍童”原来是草堆的意思,古代用它作为长方体棱台(上、下底面均为矩形额棱台)的专用术语,关于“刍童”体积计算的描述,《九章算术》注曰:“倍上表,下表从之,亦倍小表,上表从之,各以其广乘之,并,以高若深乘之,皆六面一.”其计算方法是:将上底面的长乘二,与下底面的长相加,再与上底面的宽相乘;将下底面的长乘二,与上底面的长相加,再与下底面的宽相乘;把这两个数值相加,与高相乘,再取其六分之一,以此算法,现有上下底面为相似矩形的棱台,相似比为![]() ,高为3,且上底面的周长为6,则该棱台的体积的最大值是( )
,高为3,且上底面的周长为6,则该棱台的体积的最大值是( )
A. 14 B. 56 C. ![]() D. 63
D. 63
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com