
����Ŀ������һ��ר�ұ���ᣬ����ʦ���ף��ң���������λͬѧ�μӣ�������һ������λ�ÿ���ר�ҽ����뽻��������ʦ����ÿ��ͬѧ����ȥ�����λ�ã���˸���һ�����⣬˭�ܲ¶ԣ�˭ȥ�����λ��.�������£�ij��10λͬѧ�μ�һ��ȫ�꼶�ĸ߶���ѧ���������һ����ֻ��6��ͬѧ![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �������ˣ�������6����ֻ��1�˴����.������ĸ�ͬѧ�����²����£��ײ£�
�������ˣ�������6����ֻ��1�˴����.������ĸ�ͬѧ�����²����£��ײ£�![]() ��
��![]() ����ˣ��Ҳ£�
����ˣ��Ҳ£�![]() �����ܴ�ԣ����£�
�����ܴ�ԣ����£�![]() ��
��![]() ��
��![]() ���б���1�˴���ˣ����£�
���б���1�˴���ˣ����£�![]() ��
��![]() ��
��![]() �������ܴ�ԣ������ǻش��������ʦ˵������ֻ��1�˲¶ԣ�������ʦ������λ�ø���__________��
�������ܴ�ԣ������ǻش��������ʦ˵������ֻ��1�˲¶ԣ�������ʦ������λ�ø���__________��
 ���ɶ���ܲ��¿�ֱͨ�߿�ϵ�д�
���ɶ���ܲ��¿�ֱͨ�߿�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������![]() �;���
�;���![]() ���ڵ�ƽ�滥�ഹֱ��
���ڵ�ƽ�滥�ഹֱ��![]() ��
��![]() ��
��![]() ���߶�
���߶�![]() ���е㣮
���е㣮
��1����֤��![]() ƽ��
ƽ��![]() ��
��
��2����![]() ��������
��������![]() �Ĵ�С��
�Ĵ�С��
��3�����߶�![]() ���ܴ���һ��
���ܴ���һ��![]() ��ʹ��
��ʹ��![]() ����
����![]() �����ֵ��
�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Բ![]() �����ҽ���ֱ�Ϊ
�����ҽ���ֱ�Ϊ![]() ��
��![]() ������
������![]() ��ֱ��
��ֱ��![]() ����Բ���ڵ�
����Բ���ڵ�![]() ��
��![]() ��
��![]() ���ܳ�Ϊ
���ܳ�Ϊ![]() .
.
��1������Բ�ı����̣�
��2����![]() .�ٵ�
.�ٵ�![]() ʱ����ֱ��
ʱ����ֱ��![]() �ķ��̣�
�ķ��̣�
��֤��![]() �Ƕ�ֵ��������˶�ֵ.
�Ƕ�ֵ��������˶�ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() ��ƽ��ֱ������ϵ��������ͬ���ĵ�,��
��ƽ��ֱ������ϵ��������ͬ���ĵ�,��![]() ,
,![]() ,��
,��![]() �����
�����![]() ���ͷָ�
���ͷָ�![]() .��֪ƽ���ϵĵ�
.��֪ƽ���ϵĵ�![]() ���ͷָ��
���ͷָ��![]() ��������˵����ȷ����
��������˵����ȷ����
A. ![]() �����߶�
�����߶�![]() ���е�
���е�
B. ![]() �����߶�
�����߶�![]() ���е�
���е�
C. ![]() ����ͬʱ���߶�
����ͬʱ���߶�![]() ��
��
D. ![]() ������ͬʱ���߶�
������ͬʱ���߶�![]() ���ӳ�����
���ӳ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
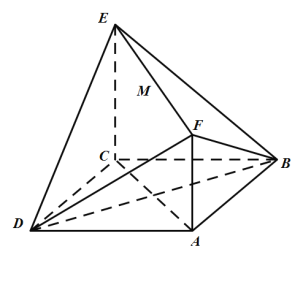
����Ŀ����ͼ��������P��ABCD�У�����ABCD�����Σ�PD��ƽ��ABCD��PD=AD=3��PM=2MD��AN=2NB����DAB=60�㣮
��1����֤��ֱ��AM��ƽ��PNC��
��2��������D��PC��N������ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����չ���ƹ���Ĺ涨������ƹ������ֱ�����������£�����Ϊ2.7�ˣ������������������![]() �ھ���Ϊ�Ǻϸ��Ʒ��������������������������
�ھ���Ϊ�Ǻϸ��Ʒ��������������������������![]() ������̬�ֲ�.�ִ�ij��������һ����Ʒ�������ȡ10�����������������£�
������̬�ֲ�.�ִ�ij��������һ����Ʒ�������ȡ10�����������������£�
2.72 2.68 2.7 2.75 2.66 2.7 2.6 2.69 2.7 2.8
��1����������10����Ʒ������ƽ����![]() ������
������![]() ��
��
��2�������ã�1�������ƽ����![]() ������
������![]() ������������Ʒ�ĺϸ����ܷ�ﵽ
������������Ʒ�ĺϸ����ܷ�ﵽ![]() ��
��
�������Ʒ����������̬�ֲ�![]() ����ô��������Ʒ�������ȡ10����Ʒ�����в��ϸ��Ʒ�ĸ���Ϊ����.���������������
����ô��������Ʒ�������ȡ10����Ʒ�����в��ϸ��Ʒ�ĸ���Ϊ����.���������������![]() ������̬�ֲ�
������̬�ֲ�![]() ����
����![]() ��
��![]() ��
��![]() .
.![]() ��0.6277��
��0.6277��![]() ��0.9743�ֱ������㣩
��0.9743�ֱ������㣩
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�����ڽ�A��B��C���Եı߷ֱ�Ϊa��b��c����cosA=![]() cosB��b=
cosB��b=![]() ��c=4��M��N�DZ�AC�ϵ��������㣬��AM=2CN����
��c=4��M��N�DZ�AC�ϵ��������㣬��AM=2CN����![]() �����ֵΪ______��
�����ֵΪ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������2017��11��-2018��11��ij������ҵԭ�Ͳ������¶�����ͼ��������˵����ȷ���ǣ� ��
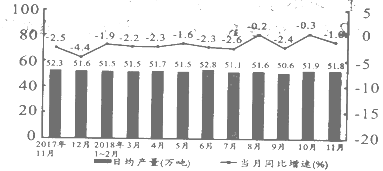
A. 2018��11�·�ԭ�Ͳ���ԼΪ51.8���
B. 2018��11�·�ԭ�Ͳ������2017��11������1.0%
C. 2018��11�·�ԭ�Ͳ��������¼���54.9���
D. 2018��1-11�·�ԭ�͵��ܲ�������15000���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com