
【题目】已知函数![]() ,
,![]() 是
是![]() 的导函数,
的导函数,![]() .
.
(1)当![]() 时,判断函数
时,判断函数![]() 在
在![]() 上是否存在零点,并说明理由;
上是否存在零点,并说明理由;
(2)若![]() 在
在![]() 上存在最小值,求
上存在最小值,求![]() 的取值范围.
的取值范围.
【答案】(1)不存在零点,理由见解析;(2)![]()
【解析】
(1)当![]() 时,得
时,得![]() ,对
,对![]() 求导,从而得单调性,即可判断零点;
求导,从而得单调性,即可判断零点;
(2)求出![]() 的导函数,结合
的导函数,结合![]() ,
,![]() 讨论
讨论![]() 的单调性,看
的单调性,看![]() 是否存在最值即可得到答案.
是否存在最值即可得到答案.
(1)![]() 时,
时,![]() .
.
令![]() ,即
,即![]() ,
,![]() ,得
,得![]() ,
,
当![]() 变化时,
变化时,![]() ,
,![]() 变化如下:
变化如下:
|
|
|
|
| - | 0 | + |
| 减 | 最小值 | 增 |
∴函数![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() .
.
∴![]() 的极小值为
的极小值为![]() .∴函数
.∴函数![]() 在
在![]() 上不存在零点.
上不存在零点.
(2)因为![]() ,所以
,所以![]() ,
,
令![]() ,则
,则![]() .
.
①当![]() 时,
时,![]() ,即
,即![]() ,
,
∴![]() 在
在![]() 单调递增,
单调递增,
∴![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 单调递增,∴
单调递增,∴![]() 在
在![]() 不存在最小值,
不存在最小值,
②当![]() 时,
时,![]() ,
,
所以![]() ,即
,即![]() 在
在![]() 内有唯一解
内有唯一解![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
所以![]() ,又因为
,又因为![]() ,
,
所以![]() 在
在![]() 内有唯一零点
内有唯一零点![]() ,
,
当![]() 时,
时,![]() 即
即![]() ,
,
当![]() 时,
时,![]() 即
即![]() ,所以
,所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
所以函数![]() 在
在![]() 处取得最小值,
处取得最小值,
即![]() 时,函数
时,函数![]() 在
在![]() 上存在最小值.
上存在最小值.
综上所述,![]() 在
在![]() 上存在最小值时,
上存在最小值时,![]() 的取值范围为
的取值范围为![]() .
.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
【题目】若数列![]() 的每一项都不等于零,且对于任意的
的每一项都不等于零,且对于任意的![]() ,都有
,都有![]() (
(![]() 为常数),则称数列
为常数),则称数列![]() 为“类等比数列”;已知数列
为“类等比数列”;已知数列![]() 满足:
满足:![]()
![]() ,对于任意的
,对于任意的![]() ,都有
,都有![]() ;
;
(1)求证:数列![]() 是“类等比数列”;
是“类等比数列”;
(2)若![]() 是单调递减数列,求实数
是单调递减数列,求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,求数列
,求数列![]() 的前
的前![]() 项之积取最大值时
项之积取最大值时![]() 的值;
的值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市《城市总体规划(![]() 年)》提出到
年)》提出到![]() 年实现“
年实现“![]() 分钟社区生活圈”全覆盖的目标,从教育与文化、医疗与养老、交通与购物、休闲与健身
分钟社区生活圈”全覆盖的目标,从教育与文化、医疗与养老、交通与购物、休闲与健身![]() 个方面构建“
个方面构建“![]() 分钟社区生活圈”指标体系,并依据“
分钟社区生活圈”指标体系,并依据“![]() 分钟社区生活圈”指数高低将小区划分为:优质小区(指数为
分钟社区生活圈”指数高低将小区划分为:优质小区(指数为![]() )、良好小区(指数为
)、良好小区(指数为![]() )、中等小区(指数为
)、中等小区(指数为![]() )以及待改进小区(指数为
)以及待改进小区(指数为![]() )
)![]() 个等级.下面是三个小区
个等级.下面是三个小区![]() 个方面指标的调查数据:
个方面指标的调查数据:
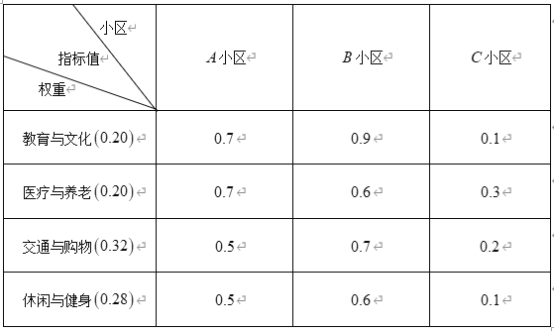
注:每个小区“![]() 分钟社区生活圈”指数
分钟社区生活圈”指数![]() ,其中
,其中![]() 、
、![]() 、
、![]() 、
、![]() 为该小区四个方面的权重,
为该小区四个方面的权重,![]() 、
、![]() 、
、![]() 、
、![]() 为该小区四个方面的指标值(小区每一个方面的指标值为
为该小区四个方面的指标值(小区每一个方面的指标值为![]() 之间的一个数值).
之间的一个数值).
现有![]() 个小区的“
个小区的“![]() 分钟社区生活圈”指数数据,整理得到如下频数分布表:
分钟社区生活圈”指数数据,整理得到如下频数分布表:
分组 |
|
|
|
|
|
频数 |
|
|
|
|
|
(Ⅰ)分别判断![]() 、
、![]() 、
、![]() 三个小区是否是优质小区,并说明理由;
三个小区是否是优质小区,并说明理由;
(Ⅱ)对这![]() 个小区按照优质小区、良好小区、中等小区和待改进小区进行分层抽样,抽取
个小区按照优质小区、良好小区、中等小区和待改进小区进行分层抽样,抽取![]() 个小区进行调查,若在抽取的
个小区进行调查,若在抽取的![]() 个小区中再随机地选取
个小区中再随机地选取![]() 个小区做深入调查,记这
个小区做深入调查,记这![]() 个小区中为优质小区的个数
个小区中为优质小区的个数![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题P:函数![]() 且|f(a)|<2,命题Q:集合A={x|x2+(a+2)x+1=0,x∈R},B={x|x>0}且A∩B=,
且|f(a)|<2,命题Q:集合A={x|x2+(a+2)x+1=0,x∈R},B={x|x>0}且A∩B=,
(1)分别求命题P、Q为真命题时的实数a的取值范围;
(2)当实数a取何范围时,命题P、Q中有且仅有一个为真命题;
(3)设P、Q皆为真时a的取值范围为集合S,![]() ,若RTS,求m的取值范围.
,若RTS,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程。
已知曲线C![]() :
:![]() (t为参数), C
(t为参数), C![]() :
:![]() (
(![]() 为参数)。
为参数)。
(1)化C![]() ,C
,C![]() 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)若C![]() 上的点P对应的参数为
上的点P对应的参数为![]() ,Q为C
,Q为C![]() 上的动点,求
上的动点,求![]() 中点
中点![]() 到直线
到直线
![]() (t为参数)距离的最小值。
(t为参数)距离的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,沿河有A、B两城镇,它们相距![]() 千米.以前,两城镇的污水直接排入河里,现为保护环境,污水需经处理才能排放.两城镇可以单独建污水处理厂,或者联合建污水处理厂(在两城镇之间或其中一城镇建厂,用管道将污水从各城镇向污水处理厂输送).依据经验公式,建厂的费用为
千米.以前,两城镇的污水直接排入河里,现为保护环境,污水需经处理才能排放.两城镇可以单独建污水处理厂,或者联合建污水处理厂(在两城镇之间或其中一城镇建厂,用管道将污水从各城镇向污水处理厂输送).依据经验公式,建厂的费用为![]() (万元),
(万元),![]() 表示污水流量;铺设管道的费用(包括管道费)
表示污水流量;铺设管道的费用(包括管道费)![]() (万元),
(万元),![]() 表示输送污水管道的长度(千米).已知城镇A和城镇B的污水流量分别为
表示输送污水管道的长度(千米).已知城镇A和城镇B的污水流量分别为![]() 、
、![]() ,
,![]() 、
、![]() 两城镇连接污水处理厂的管道总长为
两城镇连接污水处理厂的管道总长为![]() 千米.假定:经管道输送的污水流量不发生改变,污水经处理后直接排入河中.请解答下列问题(结果精确到
千米.假定:经管道输送的污水流量不发生改变,污水经处理后直接排入河中.请解答下列问题(结果精确到![]() ):
):
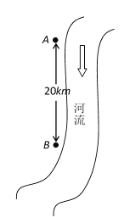
(1)若在城镇A和城镇B单独建厂,共需多少总费用?
(2)考虑联合建厂可能节约总投资,设城镇A到拟建厂的距离为![]() 千米,求联合建厂的总费用
千米,求联合建厂的总费用![]() 与
与![]() 的函数关系式,并求
的函数关系式,并求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在我们的教材必修一中有这样一个问题,假设你有一笔资金,现有三种投资方案供你选择,这三种方案的回报如下:
方案一:每天回报![]() 元;
元;
方案二:第一天回报![]() 元,以后每天比前一天多回报
元,以后每天比前一天多回报![]() 元;
元;
方案三:第一天回报![]() 元,以后每天的回报比前一天翻一番.
元,以后每天的回报比前一天翻一番.
记三种方案第![]() 天的回报分别为
天的回报分别为![]() ,
,![]() ,
,![]() .
.
(1)根据数列的定义判断数列![]() ,
,![]() ,
,![]() 的类型,并据此写出三个数列的通项公式;
的类型,并据此写出三个数列的通项公式;
(2)小王准备做一个为期十天的短期投资,他应该选择哪一种投资方案?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com