已知三次函数f(x)的导函数f′(x)=3x2-3ax,f(0)=b,a、b为实数.
(1)若曲线y=f(x)在点(a+1,f(a+1))处切线的斜率为12,求a的值;
(2)若f(x)在区间[-1,1]上的最小值、最大值分别为-2、1,且1<a<2,求函数f(x)的解析式.
【答案】
分析:(1)求出x=a+1处的导数值即切线的斜率,令其为12,列出方程,求出a的值.
(2)据导函数的形式设出f(x),求出导函数为0的两个根,判断出根与定义域的关系,求出函数的最值,列出方程求出f(x)的解析式.
解答:解:(1)由导数的几何意义f′(a+1)=12
∴3(a+1)
2-3a(a+1)=12
∴3a=9∴a=3
(2)∵f′(x)=3x
2-3ax,f(0)=b
∴
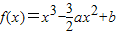
由f′(x)=3x(x-a)=0得x
1=0,x
2=a
∵x∈[-1,1],1<a<2
∴当x∈[-1,0)时,f′(x)>0,f(x)递增;当x∈(0,1]时,f′(x)<0,f(x)递减.
∴f(x)在区间[-1,1]上的最大值为f(0)
∵f(0)=b,
∴b=1
∵
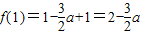
,
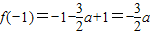
∴f(-1)<f(1)
∴f(-1)是函数f(x)的最小值,
∴
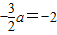
∴
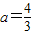
∴f(x)=x
3-2x
2+1
点评:曲线在切点处的导数值为曲线的切线斜率;求函数的最值,一定要注意导数为0的根与定义域的关系.

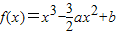
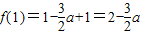 ,
,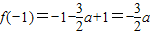
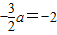
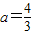


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案