
【题目】已知函数![]()
(1)求函数![]() 的定义域;
的定义域;
(2)判断函数![]() 的奇偶性。
的奇偶性。
【答案】(1){x|﹣1<x<1}(2)偶函数
【解析】
(1)要求函数f(x)+g(x)的定义域,我们可根据让函数解析式有意义的原则,构造不等式组,解不等式组即可得到函数f(x)+g(x)的定义域;
(2)要判断h(x)=f(x)+g(x)的奇偶性,我们根据奇偶性的定义,先判断其定义域是否关于原点对称,然后再判断f(﹣x)+g(﹣x)与f(x)+g(x)的关系,结合奇偶性的定义进行判断;
(1)f(x)+g(x)=![]() +
+![]() .
.
若要上式有意义,则![]() ,
,
即﹣1<x<1.
所以所求定义域为{x|﹣1<x<1}
(2)记h(x)=f(x)+g(x),定义域为{x|﹣1<x<1}
则h(﹣x)=f(﹣x)+g(﹣x)
=log2(﹣x+1)+log2(1+x)=h(x).
所以h(x)=f(x)+g(x)是偶函数.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣ ![]() x3+
x3+ ![]() x2﹣2x(a∈R)
x2﹣2x(a∈R)
(1)当a=3时,求函数f(x)的单调区间;
(2)若对于任意x∈[1,+∞)都有f′(x)<2(a﹣1)成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的方程为ρsin(θ+ ![]() )=
)= ![]() ,圆C的方程为
,圆C的方程为 ![]() (θ为参数).
(θ为参数).
(1)把直线l和圆C的方程化为普通方程;
(2)求圆C上的点到直线l距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度![]() (单位:千克/年)是养殖密度
(单位:千克/年)是养殖密度![]() (单位:尾/立方米)的函数.当
(单位:尾/立方米)的函数.当![]() 不超过
不超过![]() 尾/立方米时,
尾/立方米时, ![]() 的值为
的值为![]() 千克/年;当
千克/年;当![]() 时,
时, ![]() 是
是![]() 的一次函数,且当
的一次函数,且当![]() 时,
时, ![]() .
.
(![]() )当
)当![]() 时,求
时,求![]() 关于
关于![]() 的函数的表达式.
的函数的表达式.
(![]() )当养殖密度
)当养殖密度![]() 为多大时,每立方米的鱼的年生长量(单位:千克/立方米)可以达到最大?并求出最大值.
为多大时,每立方米的鱼的年生长量(单位:千克/立方米)可以达到最大?并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设椭圆的中心为原点![]() ,长轴在
,长轴在![]() 轴上,上顶点为
轴上,上顶点为![]() ,左,右焦点分别为
,左,右焦点分别为![]() ,线段
,线段![]() 的中点分别为
的中点分别为![]() ,且
,且![]() 是面积为4的直角三角形.
是面积为4的直角三角形.
(1)求该椭圆的离心率和标准方程;
(2)过![]() 做直线
做直线![]() 交椭圆于
交椭圆于![]() 两点,使
两点,使![]() ,求直线
,求直线![]() 的方程.
的方程.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点列An(an , bn)(n∈N*)均为函数y=ax(a>0,a≠1)的图象上,点列Bn(n,0)满足|AnBn|=|AnBn+1|,若数列{bn}中任意连续三项能构成三角形的三边,则a的取值范围为( )
A.(0, ![]() )∪(
)∪( ![]() ,+∞)
,+∞)
B.( ![]() ,1)∪(1,
,1)∪(1, ![]() )
)
C.(0, ![]() )∪(
)∪( ![]() ,+∞)
,+∞)
D.( ![]() ,1)∪(1,
,1)∪(1, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆C: ![]() +
+ ![]() =1(a>b>0)的离心率是
=1(a>b>0)的离心率是 ![]() ,且过点(
,且过点( ![]() ,
, ![]() ).设点A1 , B1分别是椭圆的右顶点和上顶点,如图所示过 点A1 , B1引椭圆C的两条弦A1E、B1F.
).设点A1 , B1分别是椭圆的右顶点和上顶点,如图所示过 点A1 , B1引椭圆C的两条弦A1E、B1F.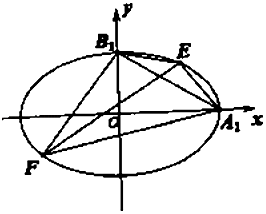
(1)求椭圆C的方程;
(2)若直线A1E与B1F的斜率是互为相反数.
①求直线EF的斜率k0②设直线EF的方程为y=k0x+b(﹣1≤b≤1)设△A1EF、△B1EF的面积分别为S1和S2 , 求S1+S2的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , Sn=n2+2n,bn=anan+1cos(n+1)π,数列{bn} 的前n项和为Tn , 若Tn≥tn2对n∈N*恒成立,则实数t的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某个体经营者把开始六个月试销A、B两种商品的逐月投资与所获纯利润列成下表:
投资A商品金额(万元) | 1 | 2 | 3 | 4 | 5 | 6 |
获纯利润(万元) | 0.65 | 1.39 | 1.85 | 2 | 1.84 | 1.40 |
投资B商品金额(万元) | 1 | 2 | 3 | 4 | 5 | 6 |
获纯利润(万元) | 0.25 | 0.49 | 0.76 | 1 | 1.26 | 1.51 |
该经营者准备下月投入12万元经营这两种产品,但不知投入A、B两种商品各多少才最合算.请你帮助制定一下资金投入方案,使得该经营者能获得最大利润,并按你的方案求出该经营者下月可获得的最大利润(结果保留两个有效数字).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com