
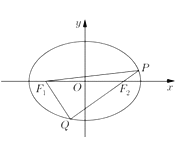
【题目】已知椭圆![]() 的左右焦点为
的左右焦点为![]() ,过
,过![]() (M不过椭圆的顶点和中心)且斜率为k直线l交椭圆于
(M不过椭圆的顶点和中心)且斜率为k直线l交椭圆于![]() 两点,与y轴交于点N,且
两点,与y轴交于点N,且![]() .
.
(1)若直线l过点![]() ,求
,求![]() 的周长;
的周长;
(2)若直线l过点![]() ,求线段
,求线段![]() 的中点R的轨迹方程;
的中点R的轨迹方程;
(3)求证:![]() 为定值,并求出此定值.
为定值,并求出此定值.
科目:高中数学 来源: 题型:
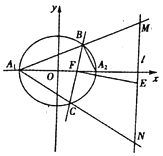
【题目】如图,已知椭圆![]()
![]() 的长轴
的长轴![]() ,长为4,过椭圆的右焦点
,长为4,过椭圆的右焦点![]() 作斜率为
作斜率为![]() (
(![]() )的直线交椭圆于
)的直线交椭圆于![]() 、
、![]() 两点,直线
两点,直线![]() ,
,![]() 的斜率之积为
的斜率之积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() ,直线
,直线![]() ,
,![]() 分别与
分别与![]() 相交于
相交于![]() 、
、![]() 两点,设
两点,设![]() 为线段
为线段![]() 的中点,求证:
的中点,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是![]() 的中点.
的中点.

(1)设P是![]() 上的一点,且AP⊥BE,求∠CBP的大小;
上的一点,且AP⊥BE,求∠CBP的大小;
(2)当AB=3,AD=2时,求二面角E-AG-C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某款冰淇淋的包装盒为圆台,盒盖为直径为![]() 的圆形纸片,每盒冰淇淋中包含有香草口味、巧克力口味和草莓口味冰淇淋球各一个,假定每个冰淇淋球都是半径为
的圆形纸片,每盒冰淇淋中包含有香草口味、巧克力口味和草莓口味冰淇淋球各一个,假定每个冰淇淋球都是半径为![]() 的球体,三个冰淇淋球两两相切,且都与冰淇淋盒盖、盒底和盒子侧面的曲面相切,则冰淇淋盒的体积为______.
的球体,三个冰淇淋球两两相切,且都与冰淇淋盒盖、盒底和盒子侧面的曲面相切,则冰淇淋盒的体积为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
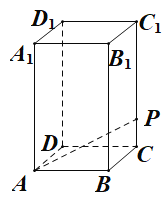
【题目】如图,在底面边长为![]() ,侧棱长为
,侧棱长为![]() 的正四棱柱
的正四棱柱![]() 中,
中,![]() 是侧棱
是侧棱![]() 上的一点,
上的一点,![]() .
.
(1)若![]() ,求异面直线
,求异面直线![]() 与
与![]() 所成角的余弦;
所成角的余弦;
(2)是否存在实数![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成角的正弦值是
所成角的正弦值是![]() ?若存在,请求出
?若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市《城市总体规划(![]() 年)》提出到
年)》提出到![]() 年实现“
年实现“![]() 分钟社区生活圈”全覆盖的目标,从教育与文化、医疗与养老、交通与购物、休闲与健身
分钟社区生活圈”全覆盖的目标,从教育与文化、医疗与养老、交通与购物、休闲与健身![]() 个方面构建“
个方面构建“![]() 分钟社区生活圈”指标体系,并依据“
分钟社区生活圈”指标体系,并依据“![]() 分钟社区生活圈”指数高低将小区划分为:优质小区(指数为
分钟社区生活圈”指数高低将小区划分为:优质小区(指数为![]() )、良好小区(指数为
)、良好小区(指数为![]() )、中等小区(指数为
)、中等小区(指数为![]() )以及待改进小区(指数为
)以及待改进小区(指数为![]() )
)![]() 个等级.下面是三个小区
个等级.下面是三个小区![]() 个方面指标的调查数据:
个方面指标的调查数据:
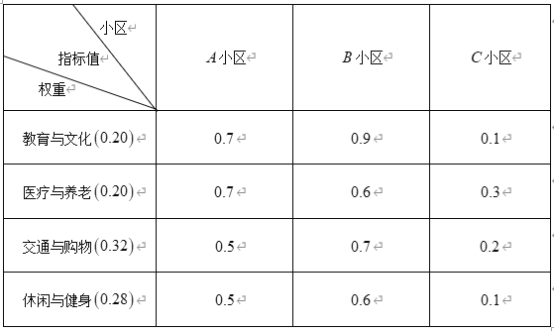
注:每个小区“![]() 分钟社区生活圈”指数
分钟社区生活圈”指数![]() ,其中
,其中![]() 、
、![]() 、
、![]() 、
、![]() 为该小区四个方面的权重,
为该小区四个方面的权重,![]() 、
、![]() 、
、![]() 、
、![]() 为该小区四个方面的指标值(小区每一个方面的指标值为
为该小区四个方面的指标值(小区每一个方面的指标值为![]() 之间的一个数值).
之间的一个数值).
现有![]() 个小区的“
个小区的“![]() 分钟社区生活圈”指数数据,整理得到如下频数分布表:
分钟社区生活圈”指数数据,整理得到如下频数分布表:
分组 |
|
|
|
|
|
频数 |
|
|
|
|
|
(Ⅰ)分别判断![]() 、
、![]() 、
、![]() 三个小区是否是优质小区,并说明理由;
三个小区是否是优质小区,并说明理由;
(Ⅱ)对这![]() 个小区按照优质小区、良好小区、中等小区和待改进小区进行分层抽样,抽取
个小区按照优质小区、良好小区、中等小区和待改进小区进行分层抽样,抽取![]() 个小区进行调查,若在抽取的
个小区进行调查,若在抽取的![]() 个小区中再随机地选取
个小区中再随机地选取![]() 个小区做深入调查,记这
个小区做深入调查,记这![]() 个小区中为优质小区的个数
个小区中为优质小区的个数![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)若![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() ;
;
(2)若![]() ,求曲线
,求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com