练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数在与时都取得极值.（1）求的值；（2）若对， 恒成立，求的取值范围

    【答案】(1) (2)

    【解析】试题分析：（1）求出导函数，通过和为的两根，得到方程组求解即可；（2）化简函数，求出导函数，通过当时，当时，当时， ，当时， ，判断函数的单调性，求出函数的极值，然后求解的取值范围.

    试题解析：（1）∵，由已知条件可知： 和1为的两根，

    由韦达定理得： ，∴，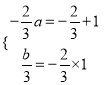

    （2）由（1）得： ，由题知：当 (－2， )时，

    ∴函数在区间(－2， )上是增函数；

    当 (，1)时， ，∴函数在(，1)上是减函数；

    当 (1，2)时， ，∴函数在(1，2)上是增函数，

    ∴当时， ；当时，

    ∵，∴ [－2，2]时， ，

    由在 [－2，2]时， 恒成立得：

    由此解得：

    ∴的取值范围为：(， ]∪[2， )

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知四棱锥中，底面为直角梯形， 平面，侧面是等腰直角三角形， ， ，点是棱的中点．

    （1）证明：平面平面；

    （2）求锐二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】数列的前项和为，．

    （）证明数列是等比数列，求出数列的通项公式．

    （）设，求数列的前项和．

    （）数列中是否存在三项，它们可以构成等比数列？若存在，求出一组符合条件的项；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（题文）（题文）“你低碳了吗？”这是某市为倡导建设节约型社会而发布的公益广告里的一句话，活动组织者为了了解这则广告的宣传效果，随机抽取了120名年龄在，，…，的市民进行问卷调查，由此得到的样本的频率分布直方图如图所示.

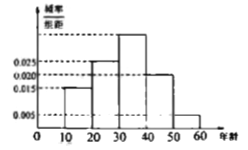
    （1）根据直方图填写频率分布统计表；

    （2）根据直方图，试估计受访市民年龄的中位数（保留整数）；

    （3）如果按分层抽样的方法，在受访市民样本年龄在中共抽取5名市民，再从这5人中随机选2人作为本次活动的获奖者，求年龄在和的受访市民恰好各有一人获奖的概率.

    分组

    频数

    频率

    18

    0.15

    30

    0.2

    6

    0.05

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆： 的上下两个焦点分别为，过点与轴垂直的直线交椭圆于两点， 的面积为，椭圆的离心率为．

    （1）求椭圆的标准方程；

    （2）已知为坐标原点，直线与轴交于点，与椭圆交于两个不同的点，若，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

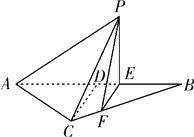
    【题目】如图所示，等腰的底边，高，点是线段上异于点的动点，点在边上，且，现沿将△折起到△的位置，使，记， 表示四棱锥的体积．

    (1)求的表达式；(2)当为何值时， 取得最大,并求最大值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数.

    （1）当时，求函数的最大值；

    （2）令，其图象上存在一点，使此处切线的斜率，求实数的取值范围；

    （3）当， 时，方程有唯一实数解，求正数的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知正方形的中心为点, 边所在的直线方程为.

    （1）求边所在的直线方程和正方形外接圆的方程；

    （2）若动圆过点,且与正方形外接圆外切,求动圆圆心的轨迹方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】直线l过点(1,0)且被两条平行直线l1：3x＋y－6＝0和l2：3x＋y＋3＝0所截得的线段长为，求直线l的方程．

    查看答案和解析>>

    同步练习册答案