练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知
    a
    =（2，4，x），
    b
    =（2，y，2），若|
    a
    |=6，
    a
    ⊥
    b
    ，则x+y的值是（　　）
    A、-3或1B、3或-1
    C、-3D、1
    考点：平面向量数量积的运算
    专题：计算题,空间向量及应用
    分析：运用向量的模的公式，可得x，再由向量垂直的条件：数量积为0，可得y，进而得到x+y的值．
    解答： 解：由
    a
    =（2，4，x），|
    a
    |=6，
    则
    		4+16+x2
    =6，解得x=±4，
    又
    b
    =（2，y，2），且
    a
    ⊥
    b
    ，
    则
    a
    •
    b
    =0，即有4+4y+2x=0，
    即y=-
    x+2
    2
    ．
    当x=4时，y=-3，有x+y=1；
    当x=-4时，y=1，有x+y=-3．
    故选A．
    点评：本题考查空间向量的数量积的性质，考查向量的模的公式，考查向量垂直的条件，考查运算能力，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知α，β∈(
    π
    2
    ，π)    ，M（Rcosα，Rsinα），N（Rcosβ，Rsinβ），则直线MN的倾斜角为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

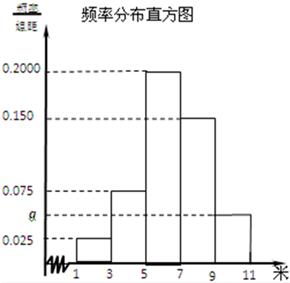    为了解高一年级女生的身体状况，从该高一年级女生中抽取一部分进行“掷铅球”的项目测试，把获得的数据分成[1，3）[3，5）[5，7）[7，9）[9，11）五组（假设测试成绩都不超过11米），画出的频率分布直方图如图所示．已知有4名学生的成绩在9米到11米之间．
    （1）求实数a的值及参加“掷铅球”项目测试的人数；
    （2）若从此次测试成绩最好和最差的两组中随机抽取2名学生再进行其它项目的测试，求所抽取的2名学生自不同组的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    a，b，c分别为△ABC三个内角A，B，C的对边，bcosC+
    		3
    bsinC-a-c=0
    （1）求证A，B，C成等差数列；
    （2）若a=2，△ABC的面积为
    		3
    ，求b，c；
    （3）若a，b，c成等比数列，求sinAsinC的值；
    （4）求sinA+sinC的取值范围；
    （5）若b=
    		3
    ，求2a+c的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

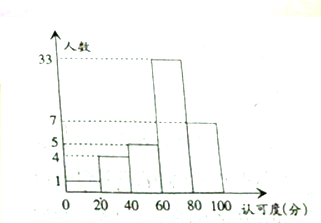    某校为了了解新的一轮教改模式有效性的“认可度”，在全校师生（可认为很多人）进行了“认可度”的问卷调查，现随机抽查50名师生，对他们的“认可度”统计分析得如图
    （1）求这50名师生的“认可度”的平均值（每一区间取中点值计算）
    （2）设表中个区间“认可度”分数的中点值构成集合A，那么从集合A中任取一值，记下该值后放回，然后再随机任选一个又记下该值后又放回，设第一次的值记为x，第二次的值记为y，求y＞x的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    函数f（x）=ax+1，（a＞0且a≠1）
    （1）当a=3，x∈[-1，2]时，求函数f（x）的值域；
    （2）求不等式f（x）≥1的解集．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    函数f（x）=
    log2(1-x)-2a，x≤0
    x2-4ax+a，x＞0
    有三个不同零点，则实数a的取值范围是（　　）
    A、a≤0
    B、a＞
    1
    4
    C、
    1
    4
    ＜a≤
    1
    2
    或a＜0
    D、a＞
    1
    4
    或a＜0

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=mx3-x．
    （1）讨论单调区间；
    （2）m=1时，求曲线f（x）在M（t，f（t））处的切线方程；
    （3）m=1时，设a＞0，如果过点（a，b）时做曲线f（x）的三条切线，证明-a＜b＜f（a）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知双曲线
    x2
    a2
    -
    y2
    b2
    =1（a＞0，b＞0）的右顶点和右焦点分别为A（a，0）、F（c，0），若在直线x=-
    a2
    c
    上存在点P使得∠APF=30°．则该双曲线的离心率的取值范围是（　　）
    A、（1，
    3+
    		17
    2
    ]
    B、[
    3+
    		17
    2
    ，+∞）
    C、（1，4]
    D、[4，+∞）

    查看答案和解析>>

    同步练习册答案