
【题目】如图,四棱锥P﹣ABCD中,四边形ABCD是边长为2的正方形,△PAD为等边三角形,E,F分别为PC和BD的中点,且EF⊥CD.
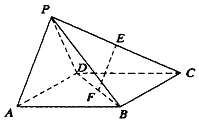
(1)证明:平面PAD⊥平面ABCD;
(2)求点C到平面PDB的距离.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)根据中位线定理可证PA⊥CD,结合AD⊥CD可得CD⊥平面PAD,于是平面PAD⊥平面ABCD;
(2)计算△PBD的面积,根据VP﹣BCD=VC﹣PBD列方程计算点C到平面PDB的距离.
(1)因为E,F分别为PC和BD的中点,所以EF∥PA,
又因为EF⊥CD,所以PA⊥CD,
因为四边形ABCD是正方形,所以AD⊥CD,
又PA∩AD=A,PA平面PAD,AD平面PAD,所以CD⊥平面PAD,
又CD平面ABCD,所以平面PAD⊥平面ABCD.
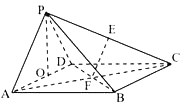
(2)取AD的中点O,连接PO,
因为△PAD是等边三角形,AD=2,所以PO⊥AD,且PO![]() ,
,
又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
所以PO⊥平面ABCD,
又四边形ABCD是边长为2的正方形,所以S△BCD![]() 2,
2,
所以VP﹣BCD![]() ,
,
连接OB,则OB![]() ,故PB
,故PB![]() 2
2![]() ,
,
又BD![]() 2
2![]() ,PD=2,
,PD=2,
所以S△PBD![]() ,
,
设C到平面PBD的距离为h,则VC﹣PBD![]() ,
,
整理得![]() ,解得h
,解得h![]() ,
,
即点C到平面PBD的距离为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
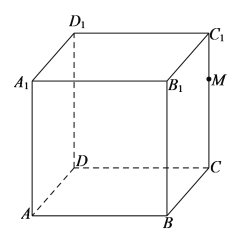
【题目】已知正方体![]() 棱长为
棱长为![]() ,如图,
,如图,![]() 为
为![]() 上的动点,
上的动点,![]() 平面
平面![]() .下面说法正确的是( )
.下面说法正确的是( )
A.直线![]() 与平面
与平面![]() 所成角的正弦值范围为
所成角的正弦值范围为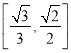
B.点![]() 与点
与点![]() 重合时,平面
重合时,平面![]() 截正方体所得的截面,其面积越大,周长就越大
截正方体所得的截面,其面积越大,周长就越大
C.点![]() 为
为![]() 的中点时,若平面
的中点时,若平面![]() 经过点
经过点![]() ,则平面
,则平面![]() 截正方体所得截面图形是等腰梯形
截正方体所得截面图形是等腰梯形
D.己知![]() 为
为![]() 中点,当
中点,当![]() 的和最小时,
的和最小时,![]() 为
为![]() 的中点
的中点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面![]() ,B,
,B,![]() ,
,![]() ,且
,且![]() ,
,![]() ,且
,且![]() ,则下列叙述错误的是( )
,则下列叙述错误的是( )
A.直线![]() 与
与![]() 是异面直线
是异面直线
B.直线![]() 在
在![]() 上的射影可能与
上的射影可能与![]() 平行
平行
C.过![]() 有且只有一个平面与
有且只有一个平面与![]() 平行
平行
D.过![]() 有且只有一个平面与
有且只有一个平面与![]() 垂直
垂直
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着![]() 年北京冬奥会临近,中国冰雪产业快速发展,冰雪运动人数快速上升,冰雪运动市场需求得到释放,将引领户外用品行业市场增长.下面是
年北京冬奥会临近,中国冰雪产业快速发展,冰雪运动人数快速上升,冰雪运动市场需求得到释放,将引领户外用品行业市场增长.下面是![]() 年至
年至![]() 年中国雪场滑雪人次(万人次)与同比增长率的统计图,则下面结论中不正确的是( )
年中国雪场滑雪人次(万人次)与同比增长率的统计图,则下面结论中不正确的是( )
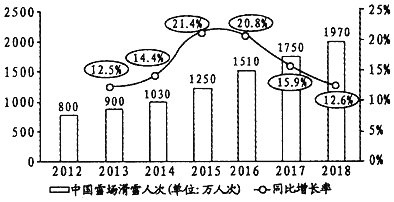
A.![]() 年至
年至![]() 年,中国雪场滑雪人次逐年增加
年,中国雪场滑雪人次逐年增加
B.![]() 年至
年至![]() 年,中国雪场滑雪人次和同比增长率均逐年增加
年,中国雪场滑雪人次和同比增长率均逐年增加
C.![]() 年与
年与![]() 年相比,中国雪场滑雪人次的同比增长率近似相等,所以同比增长人数也近似相等
年相比,中国雪场滑雪人次的同比增长率近似相等,所以同比增长人数也近似相等
D.![]() 年与
年与![]() 年相比,中国雪场滑雪人次增长率约为
年相比,中国雪场滑雪人次增长率约为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】干支纪年法是中国历法上自古以来就一直使用的纪年方法、干支是天干和地支的总称,甲、乙、丙、丁、戊、己、庚、辛、壬、癸为天干:子、丑、寅、卯、辰、已、午、未,申、西、戌、亥为地支.把十天干和十二地支依次相配,如甲对子、乙对丑、丙对寅、…癸对寅,其中天干比地支少两位,所以天干先循环,甲对戊、乙对亥、…接下来地支循环,丙对子、丁对丑、.,以此用来纪年,今年2020年是庚子年,那么中华人民共和国建国100周年即2049年是( )
A.戊辰年B.己巳年C.庚午年D.庚子年
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,以极点
,以极点![]() 为原点,极轴所在直线为
为原点,极轴所在直线为![]() 轴建立直角坐标系,过点
轴建立直角坐标系,过点![]() 作倾斜角为
作倾斜角为![]() (
(![]() )的直线
)的直线![]() 交曲线
交曲线![]() 于
于![]() 、
、![]() 两点.
两点.
(1)求曲线![]() 的直角坐标方程,并写出直线
的直角坐标方程,并写出直线![]() 的参数方程;
的参数方程;
(2)过点![]() 的另一条直线
的另一条直线![]() 与
与![]() 垂直,且与曲线
垂直,且与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快餐连锁店,每天以200元的价格从总店购进早餐,然后以每份10元的价格出售.40份以内,总店收成本价每份5元,当天不能出售的早餐立即以1元的价格被总店回收,超过40份的未销售的部分总店成本价回收,然后进行环保处理.如果销售超过40份,则超过40份的利润需上缴总店.该快餐连锁店记录了100天早餐的销售量(单位:份),整理得下表:
日销售量 | 25 | 30 | 35 | 40 | 45 | 50 |
频数 | 10 | 16 | 28 | 24 | 14 | 8 |
完成下列问题:
(1)写出每天获得利润![]() 与销售早餐份数
与销售早餐份数![]() (
(![]() )的函数关系式;
)的函数关系式;
(2)估计每天利润不低于150元的概率;
(3)估计该快餐店每天的平均利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)已知过原点的动直线![]() 与圆
与圆![]()
![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() .
.
(1)求圆![]() 的圆心坐标;
的圆心坐标;
(2)求线段![]() 的中点
的中点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(3)是否存在实数![]() ,使得直线
,使得直线![]()
![]() 与曲线
与曲线![]() 只有一个交点?若存在,求出
只有一个交点?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com