
【题目】已知函数![]() .
.
(1)若![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,试判断函数
时,试判断函数![]() 的零点个数,并说明理由.
的零点个数,并说明理由.
【答案】(1) 见解析(2) ![]() 只有一个零点
只有一个零点
【解析】
(1)求导![]() ,对a分类比较
,对a分类比较![]() 与3的大小,求得
与3的大小,求得![]() 及
及![]() 的解集,即可求得g(x)的单调区间;
的解集,即可求得g(x)的单调区间;
(2)由(1)可知,![]() 的单增区间为
的单增区间为![]() 和
和![]() ,单减区间为
,单减区间为![]()
得到f(x)的极大值为f(1) <0,,极小值为f(3)<0,又![]() , 得到
, 得到![]() 在
在![]() 上只有一个零点.从而得到函数f(x)只有一个零点.
上只有一个零点.从而得到函数f(x)只有一个零点.
(1)![]()
当![]() 即
即![]() ,
,![]() ,
,![]()
所以![]() 的单增区间为
的单增区间为![]() 和
和![]() ,单减区间为
,单减区间为![]() ,
,
当 ![]() 即
即![]() ,
,![]() 或
或![]() ,
,![]()
所以![]() 的单增区间为
的单增区间为![]() 和
和![]() ,单减区间为
,单减区间为![]() ,
,
当![]() ,
,![]() ,所以
,所以![]() 的单增区间为(0,
的单增区间为(0,![]() ).
).
综上所述:当0<a<![]() 时,所以
时,所以![]() 的单增区间为
的单增区间为![]() 和
和![]() ,单减区间为
,单减区间为![]() ,
,
当![]() ,
,![]() 的单增区间为
的单增区间为![]() ,
,
当![]() 时,所以
时,所以![]() 的单增区间为
的单增区间为![]() 和
和![]() ,单减区间为
,单减区间为![]()
(2)当![]() 时,
时,![]() ,
,![]() ,所以由(1)可知,
,所以由(1)可知,![]() 的单增区间为
的单增区间为![]() 和
和![]() ,单减区间为
,单减区间为![]()
所以f(x)的极大值为f(1)=-1<0,,极小值为f(3)<0,
当![]() 时
时![]() , 所以
, 所以![]() 在
在![]() 上只有一个零点.
上只有一个零点.
综上,![]() 只有一个零点.
只有一个零点.


科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,椭圆C:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,短轴长是2.
,短轴长是2.
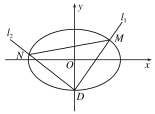
(1)求椭圆C的方程;
(2)设椭圆C的下顶点为D,过点D作两条互相垂直的直线l1,l2,这两条直线与椭圆C的另一个交点分别为M,N.设l1的斜率为k(k≠0),△DMN的面积为S,当![]() ,求k的取值范围.
,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
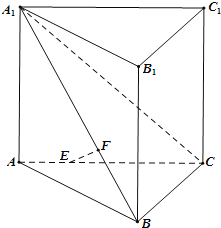
【题目】如图,在直三棱柱![]() 侧棱和底面垂直的棱柱
侧棱和底面垂直的棱柱![]() 中,平面
中,平面![]() 侧面
侧面![]() ,
,![]() ,线段AC、
,线段AC、![]() 上分别有一点E、F且满足
上分别有一点E、F且满足![]() ,
,![]() .
.
![]() 求证:
求证:![]() ;
;
![]() 求点E到直线
求点E到直线![]() 的距离;
的距离;
![]() 求二面角
求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】科学研究表明:人类对声音有不的感觉,这与声音的强度![]() 单位:瓦
单位:瓦![]() 平方米
平方米![]() 有关
有关![]() 在实际测量时,常用
在实际测量时,常用![]() 单位:分贝
单位:分贝![]() 来表示声音强弱的等级,它与声音的强度I满足关系式:
来表示声音强弱的等级,它与声音的强度I满足关系式:![]() 是常数
是常数![]() ,其中
,其中![]() 瓦
瓦![]() 平方米
平方米![]() 如风吹落叶沙沙声的强度
如风吹落叶沙沙声的强度![]() 瓦
瓦![]() 平方米,它的强弱等级
平方米,它的强弱等级![]() 分贝.
分贝.
![]() 已知生活中几种声音的强度如表:
已知生活中几种声音的强度如表:
声音来源
声音大小 | 风吹落叶沙沙声 | 轻声耳语 | 很嘈杂的马路 |
强度 |
|
|
|
强弱等级 | 10 | m | 90 |
求a和m的值
![]() 为了不影响正常的休息和睡眠,声音的强弱等级一般不能超过50分贝,求此时声音强度I的最大值.
为了不影响正常的休息和睡眠,声音的强弱等级一般不能超过50分贝,求此时声音强度I的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,![]() 是函数
是函数![]() (
(![]() ,
,![]() )图象上的任意两点,且角
)图象上的任意两点,且角![]() 的终边经过点
的终边经过点![]() ,若
,若![]() 时,
时,![]() 的最小值为
的最小值为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,可见部分如下:

试根据图表中的信息解答下列问题:
(1)求全班的学生人数及分数在[70,80)之间的频数;
(2)为快速了解学生的答题情况,老师按分层抽样的方法从位于[70,80),[80,90)和[90,100]分数段的试卷中抽取8份进行分析,再从中任选3人进行交流,求交流的学生中,成绩位于[70,80)分数段的人数X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com