
【题目】若数列![]() 满足
满足![]() 则称
则称![]() 为
为![]() 数列.记
数列.记![]()
(1)若![]() 为
为![]() 数列,且
数列,且![]() 试写出
试写出![]() 的所有可能值;
的所有可能值;
(2)若![]() 为
为![]() 数列,且
数列,且![]() 求
求![]() 的最大值;
的最大值;
(3)对任意给定的正整数![]() 是否存在
是否存在![]() 数列
数列![]() 使得
使得![]() ?若存在,写出满足条件的一个
?若存在,写出满足条件的一个![]() 数列
数列![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,见解析.
;(3)存在,见解析.
【解析】
(1)根据题意![]() ,则
,则![]() 或
或![]() ,分析后可得符合条件的
,分析后可得符合条件的![]() 数列;
数列;
(2)由于由于![]() 为
为![]() 数列,且
数列,且![]()
![]() 故n必须是不小于3的奇数. 使
故n必须是不小于3的奇数. 使![]() 最大的
最大的![]() ,可以让数列
,可以让数列![]() 先逐渐增大1,到中间位置后再逐渐减小1,由等差数列的前
先逐渐增大1,到中间位置后再逐渐减小1,由等差数列的前![]() 项和公式可得;
项和公式可得;
(3)令![]() ,则
,则![]() ,用
,用![]() 表示
表示![]() 有
有![]() ,求出
,求出![]()
![]()
![]()
![]()
![]() ,
,
![]() 是偶数,
是偶数,![]() ,则
,则![]() 是偶数,
是偶数,![]() 或
或![]() (
(![]() ),可分别求得结论.
),可分别求得结论.
(1)满足条件的![]() 数列
数列![]() ,及对应的
,及对应的![]() 分别为:
分别为:
(i) 0, 1, 2,1, 0. ![]() (ii) 0, 1, 0,1, 0.
(ii) 0, 1, 0,1, 0. ![]()
(iii) 0, 1, 0,-1, 0. ![]() (iv) 0, -1, -2,-1, 0.
(iv) 0, -1, -2,-1, 0. ![]()
(v) 0, -1, 0,-1, 0 . ![]() (vi) 0, -1, 0, 1, 0.
(vi) 0, -1, 0, 1, 0. ![]()
因此,![]() 的所有可能值为:
的所有可能值为:![]()
(2) 由于![]() 为
为![]() 数列,且
数列,且![]()
![]()
故n必须是不小于3的奇数.
于是使![]() 最大的
最大的![]() 为:
为:
![]()
这里![]() 并且
并且
![]()
因此,![]() (n为不小于3的奇数)
(n为不小于3的奇数)
(3)令![]() ,则
,则![]() 于是由
于是由![]() 得
得
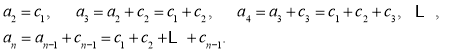
故![]()
![]()
![]()
![]()
![]()
因为![]() ,故
,故![]() 为偶数,
为偶数,
所以![]() 为偶数,
为偶数,
于是要使![]() ,必须
,必须![]() 为偶数,即
为偶数,即![]() 为4的倍数,亦即
为4的倍数,亦即
![]() 或
或![]()
(i)当![]() 时,
时,![]() 数列
数列![]() 的项在满足:
的项在满足: ![]()
![]() 时,
时,![]()
(ii)当![]() 时,
时,![]() 数列
数列![]() 的项在满足:
的项在满足:![]()
![]() 时,
时,![]()


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:
【题目】在一个给定的正![]() 边形的顶点中随机地选取三个不同的顶点,任何一种选法的可能性是相等的,则正多边形的中心位于所选三个点构成的三角形内部的概率为______.
边形的顶点中随机地选取三个不同的顶点,任何一种选法的可能性是相等的,则正多边形的中心位于所选三个点构成的三角形内部的概率为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是
是![]() 上的偶函数,对于
上的偶函数,对于![]() 都有
都有![]() 成立,且
成立,且![]() ,当
,当![]() ,
,![]() ,且
,且![]() 时,都有
时,都有![]() .则给出下列命题:①
.则给出下列命题:①![]() ;②
;②![]() 为函数
为函数![]() 图象的一条对称轴;③函数
图象的一条对称轴;③函数![]() 在
在![]() 上为减函数;④方程
上为减函数;④方程![]() 在
在![]() 上有4个根;其中正确的命题个数为( )
上有4个根;其中正确的命题个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设甲、乙两位同学上学期间,每天7:30之前到校的概率均为![]() .假定甲、乙两位同学到校情况互不影响,且任一同学每天到校情况相互独立.
.假定甲、乙两位同学到校情况互不影响,且任一同学每天到校情况相互独立.
(Ⅰ)用![]() 表示甲同学上学期间的三天中7:30之前到校的天数,求随机变量
表示甲同学上学期间的三天中7:30之前到校的天数,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)设![]() 为事件“上学期间的三天中,甲同学在7:30之前到校的天数比乙同学在7:30之前到校的天数恰好多2”,求事件
为事件“上学期间的三天中,甲同学在7:30之前到校的天数比乙同学在7:30之前到校的天数恰好多2”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于项数为m(![]() 且
且![]() )的有穷正整数数列
)的有穷正整数数列![]() ,记
,记![]()
![]() ,即
,即![]() 为
为![]() 中的最小值,设由
中的最小值,设由![]() 组成的数列
组成的数列![]() 称为
称为![]() 的“新型数列”.
的“新型数列”.
(1)若数列![]() 为2019,2020,2019,2018,2017,请写出
为2019,2020,2019,2018,2017,请写出![]() 的“新型数列”
的“新型数列”![]() 的所有项;
的所有项;
(2)若数列![]() 满足
满足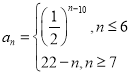 ,且其对应的“新型数列”
,且其对应的“新型数列”![]() 项数
项数![]() ,求
,求![]() 的所有项的和;
的所有项的和;
(3)若数列![]() 的各项互不相等且所有项的和等于所有项的积,求符合条件的
的各项互不相等且所有项的和等于所有项的积,求符合条件的![]() 及其对应的“新型数列”
及其对应的“新型数列”![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,
,![]() 为其前
为其前![]() 项的和,满足
项的和,满足![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:当
,求证:当![]() ,
,![]() 时
时![]() ;
;
(3)已知当![]() ,且
,且![]() 时有
时有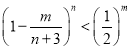 ,其中
,其中![]() ,求满足
,求满足![]() 的所有
的所有![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于由有限个自然数组成的集合A,定义集合S(A)={a+b|a∈A,b∈A},记集合S(A)的元素个数为d(S(A)).定义变换T,变换T将集合A变换为集合T(A)=A∪S(A).
(1)若A={0,1,2},求S(A),T(A);
(2)若集合A有n个元素,证明:“d(S(A))=2n-1”的充要条件是“集合A中的所有元素能组成公差不为0的等差数列”;
(3)若A{1,2,3,4,5,6,7,8}且{1,2,3,…,25,26}T(T(A)),求元素个数最少的集合A.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com