
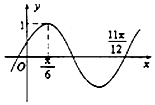
 已知函数f(x)=sinωx(ω>0),若函数y=f(x+a)(a>0)的部分图象如图所示,则ω=2,a的最小值是$\frac{π}{12}$.
已知函数f(x)=sinωx(ω>0),若函数y=f(x+a)(a>0)的部分图象如图所示,则ω=2,a的最小值是$\frac{π}{12}$. 分析 首先由图象最高点横坐标与零点的距离求函数的周期,从而由周期公式求ω,然后由图象过的已知点求出a.
解答 解:由已知函数图象得到$\frac{3}{4}T=\frac{11π}{12}-\frac{π}{6}=\frac{3}{4}$π,所以T=π,所以$ω=\frac{2π}{π}$=2,
又y=f(x+a))=sinω(x+a)且($\frac{π}{6}$,1)在图象上,
所以sin2($\frac{π}{6}$+a)=1,所以$\frac{π}{3}$+2a=2kπ$+\frac{π}{2}$,k∈Z,
所以k取0时a的最小值为$\frac{π}{12}$;
故答案为:2;$\frac{π}{12}$.
点评 本题考查了由三角函数图象求函数解析式;注意几个关键点;图象与坐标轴的交点,最高点与最低点等.


科目:高中数学 来源: 题型:选择题
 某高中体育小组共有男生24人,其50m跑成绩记作ai(i=1,2,…,24),若成绩小于6.8s为达标,则如图所示的程序框图的功能是( )
某高中体育小组共有男生24人,其50m跑成绩记作ai(i=1,2,…,24),若成绩小于6.8s为达标,则如图所示的程序框图的功能是( )| A. | 求24名男生的达标率 | B. | 求24名男生的不达标率 | ||
| C. | 求24名男生的达标人数 | D. | 求24名男生的不达标人数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
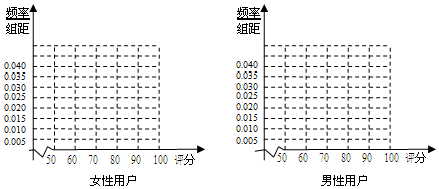
| 女性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 20 | 40 | 80 | 50 | 10 | |
| 男性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 45 | 75 | 90 | 60 | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 点D不在直线BC上 | B. | 点D在BC的延长线上 | ||
| C. | 点D在线段BC上 | D. | 点D在CB的延长线上 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象如图所示,则f(1)+f(2)+f(3)+…+f(2017)=$\sqrt{2}$.
函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象如图所示,则f(1)+f(2)+f(3)+…+f(2017)=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
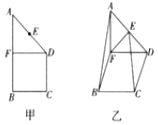 如图所示,在直角梯形ABCD中,AB∥CD,∠ABC=90°,CD=BC=1,点E为AD边上的中点,过点D作DF∥BC交AB于点F,现将此直角梯形沿DF折起,使得A-FD-B为直二面角,如图乙所示.
如图所示,在直角梯形ABCD中,AB∥CD,∠ABC=90°,CD=BC=1,点E为AD边上的中点,过点D作DF∥BC交AB于点F,现将此直角梯形沿DF折起,使得A-FD-B为直二面角,如图乙所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com