练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，四棱锥的底面是直角梯形， ， ，

    ，点在线段上，且， ， 平面.

    （1）求证：平面平面；

    （2）当四棱锥的体积最大时，求四棱锥的表面积.

    【答案】（1）见解析.

    （2）.

    【解析】【试题分析】（1）利用结合直角梯形，可知四边形是矩形，故，由于平面，所以，故平面.由此证得平面平面.（2）根据体积公式计算得，即只需取得最大值.利用基本不等式可求得的最大值为，再通过体积公式可计算得表面积.

    【试题解析】

    （1）由可得，

    易得四边形是矩形，∴，

    又平面， 平面，∴，

    又， 平面，∴平面，

    又平面，∴平面平面

    （2）四棱锥的体积为 ，

    要使四棱锥的体积取最大值，只需取得最大值.

    由条件可得，∴ ，即，

    当且仅当时， 取得最大值36.

    ， ， ，

    ，则，

    ∴，

    则四棱锥的表面积为

    .

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥V-ABC中，平面VAB平面ABC， VAB为等边三角形，ACBC且AC=BC=，O,M分别为AB,VA的中点。

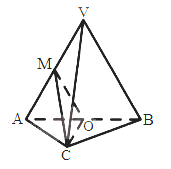
    （I）求证：VB//平面MOC；

    （II）求证：平面MOC平面VAB；

    （III）求三棱锥V-ABC的体积。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】我们知道：“心有灵犀”一般是对人的心理活动非常融洽的一种描述，它也可以用数学来定义：甲、乙两人都在{1，2，3，4，5，6}中说一个数，甲说的数记为a，乙说的数记为b，若|a﹣b|≤1，则称甲、乙两人“心有灵犀”，由此可以得到甲、乙两人“心有灵犀”的概率是（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在发生某公共卫生事件期间,有专业机构认为该事件在一段时间没有发生大规模群体感染的标准为“连续10天,每天新增疑似病例不超过7人”.根据过去10天甲、乙、丙、丁四地新增疑似病例的数据,一定符合该标准的是____.(填序号)

    ①甲地:总体均值为3,中位数为4

    ②乙地:总体均值为1,总体方差大于0

    ③丙地:中位数为2,众数为3

    ④丁地:总体均值为2,总体方差为3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】古希腊杰出的数学家丢番图的墓碑上有这样一首诗:

    这是一座古墓,里面安葬着丢番图.

    请你告诉我,丢番图的寿数几何?

    他的童年占去了一生的六分之一,

    接着十二分之一是少年时期,

    又过了七分之一的时光,他找到了自己的终身伴侣.

    五年之后,婚姻之神赐给他一个儿子,

    可是儿子不济,只活到父亲寿数的一半,就匆匆离去.

    这对父亲是一个沉重的打击,

    整整四年,为失去爱子而悲伤,

    终于告别了数学,离开了人世.

    试用循环结构,写出算法分析和算法程序.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）是定义在R上的周期为2的奇函数，当0＜x＜1时，f（x）=2x（1﹣x），则f（﹣ ）+f（1）=（ ）
    A.﹣
    B.﹣
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】袋子中放有大小和形状相同的小球若干个,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球n个.已知从袋子中随机抽取1个小球,取到标号是2的小球的概率是.

    (1)求n的值;

    (2)从袋子中不放回地随机抽取2个小球,记第一次取出的小球标号为a,第二次取出的小球标号为b.

    ①记事件A表示“a+b=2”,求事件A的概率;

    ②在区间[0,2]内任取2个实数x,y,求事件“x2+y2>(a-b)2恒成立”的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设矩形ABCD，以A、B为左右焦点，并且过C、D两点的椭圆和双曲线的离心率之积为（ ）
    A.
    B.2
    C.1
    D.条件不够，不能确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】通过随机询问110名性别不同的大学生是否爱好某项运动，得到如下的列联表：

    男

    女

    总计

    爱好

    40

    20

    60

    不爱好

    20

    30

    50

    总计

    60

    50

    110

    由 算得， ．

    P（K2≥k）

    0.050

    0.010

    0.001

    k

    3.841

    6.635

    10.828

    参照附表，得到的正确结论是（ ）
    A.在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别有关”
    B.在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别无关”
    C.有99%以上的把握认为“爱好该项运动与性别有关”
    D.有99%以上的把握认为“爱好该项运动与性别无关”

    查看答案和解析>>

    同步练习册答案