
【题目】在![]() 中,
中,![]() ,AC,AB边上的中线长之和等于9.
,AC,AB边上的中线长之和等于9.
(1)求![]() 重心M的轨迹方程;
重心M的轨迹方程;
(2)求顶点A的轨迹方程.
【答案】(1)![]() 1(y≠0);(2)
1(y≠0);(2)![]() 1(y≠0)
1(y≠0)
【解析】
(1)由已知得△ABC重心M在以B、C为两个焦点的椭圆,由此能求出△ABC重心M的轨迹方程.
(2)利用代入法,即可求顶点A的轨迹方程.
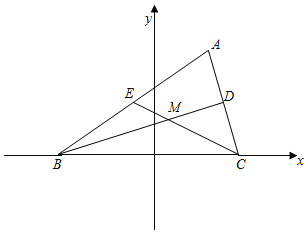
(1)如图所示,以线段BC所在直线为x轴、线段BC的中垂线为y轴建立直角坐标系
设M为△ABC的重心,BD是AC边上的中线,CE是AB边上的中线,由重心的性质知|BM|![]() |BD|,|CM|
|BD|,|CM|![]() |CE|,于是|MB|+|MC|
|CE|,于是|MB|+|MC|![]() |BD|
|BD|![]() |CE|=6
|CE|=6
根据椭圆的定义知,点M的轨迹是以B、C为焦点的椭圆.2a=6,2c=4,
∴a=3,b![]() ,
,
故所求的椭圆方程为![]() 1(y≠0)
1(y≠0)
(2)设A(x,y),则M(![]() x,
x,![]() ),代入
),代入![]() 1(y≠0),
1(y≠0),
可得出顶点A的轨迹方程为![]() 1(y≠0)
1(y≠0)


科目:高中数学 来源: 题型:
【题目】如图,直线![]() 与抛物线
与抛物线![]() (常数
(常数![]() )相交于不同的两点
)相交于不同的两点![]() 、
、![]() ,且
,且![]() (
(![]() 为定值),线段
为定值),线段![]() 的中点为
的中点为![]() ,与直线
,与直线![]() 平行的切线的切点为
平行的切线的切点为![]() (不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).
(不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).

(1)用![]() 、
、![]() 表示出
表示出![]() 点、
点、![]() 点的坐标,并证明
点的坐标,并证明![]() 垂直于
垂直于![]() 轴;
轴;
(2)求![]() 的面积,证明
的面积,证明![]() 的面积与
的面积与![]() 、
、![]() 无关,只与
无关,只与![]() 有关;
有关;
(3)小张所在的兴趣小组完成上面两个小题后,小张连![]() 、
、![]() ,再作与
,再作与![]() 、
、![]() 平行的切线,切点分别为
平行的切线,切点分别为![]() 、
、![]() ,小张马上写出了
,小张马上写出了![]() 、
、![]() 的面积,由此小张求出了直线
的面积,由此小张求出了直线![]() 与抛物线围成的面积,你认为小张能做到吗?请你说出理由.
与抛物线围成的面积,你认为小张能做到吗?请你说出理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() 上一点,经过点
上一点,经过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 、
、![]() 两点(不同于点
两点(不同于点![]() ),直线
),直线![]() 、
、![]() 分别交直线
分别交直线![]() 于点
于点![]() 、
、![]() .
.
(1)求抛物线方程及其焦点坐标;
(2)求证:以![]() 为直径的圆恰好经过原点.
为直径的圆恰好经过原点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产某种产品的年固定成本为250万元,每生产![]() 千件,需另投入成本
千件,需另投入成本![]() ,当年产量不足80千件时,
,当年产量不足80千件时,![]() (万元);当年产量不小于80千件时,
(万元);当年产量不小于80千件时,![]() (万元),每件售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(万元),每件售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过双曲线![]() 的左焦点
的左焦点![]() 作圆
作圆![]() 的切线交双曲线的右支于点
的切线交双曲线的右支于点![]() ,且切点为
,且切点为![]() ,已知
,已知![]() 为坐标原点,
为坐标原点,![]() 为线段
为线段![]() 的中点(
的中点(![]() 点在切点
点在切点![]() 的右侧),若
的右侧),若![]() 的周长为
的周长为![]() ,则双曲线的渐近线的方程为( )
,则双曲线的渐近线的方程为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
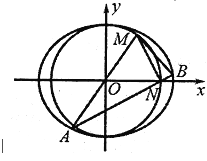
【题目】如图,椭圆![]() :
:![]() 与圆
与圆![]() :
:![]() 相切,并且椭圆
相切,并且椭圆![]() 上动点与圆
上动点与圆![]() 上动点间距离最大值为
上动点间距离最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,
,![]() ,
,![]() 与
与![]() 交于
交于![]() 两点,
两点,![]() 与圆
与圆![]() 的另一交点为
的另一交点为![]() ,求
,求![]() 面积的最大值,并求取得最大值时直线
面积的最大值,并求取得最大值时直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com