
【题目】已知![]() ,且
,且![]() .设
.设![]() 函数
函数![]() 在区间
在区间![]() 内单调递减;
内单调递减; ![]() 曲线
曲线![]() 与
与![]() 轴交于不同的两点,如果“
轴交于不同的两点,如果“![]() ”为真命题,“
”为真命题,“![]() ”为假命题,求实数
”为假命题,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
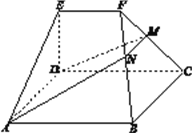
【题目】如图,在几何体![]() 中,底面
中,底面![]() 为矩形,
为矩形, ![]() ,
, ![]() .点
.点![]() 在棱
在棱![]() 上,平面
上,平面![]() 与棱
与棱![]() 交于点
交于点![]() .
.
(Ⅰ)求证: ![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)若![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,求二面角
,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(Ⅰ)抛物线的顶点在原点,坐标轴为对称轴,并经过点![]() ,求此抛物线的方程.
,求此抛物线的方程.
(Ⅱ)已知圆: ![]() (
(![]() ),把圆上的各点纵坐标不变,横坐标伸长到原来的
),把圆上的各点纵坐标不变,横坐标伸长到原来的![]() 倍得一椭圆.求椭圆方程,并证明椭圆离心率是与
倍得一椭圆.求椭圆方程,并证明椭圆离心率是与![]() 无关的常数.
无关的常数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin2( ![]() +x)+
+x)+ ![]() (sin2x﹣cos2x),x∈[
(sin2x﹣cos2x),x∈[ ![]() ,
, ![]() ].
].
(1)求 ![]() 的值;
的值;
(2)求f(x)的单调区间;
(3)若不等式|f(x)﹣m|<2恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
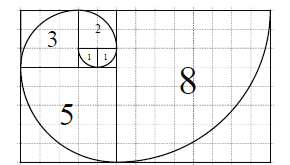
【题目】斐波那契数列![]() 满足:
满足: ![]() .若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前
.若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前![]() 项所占的格子的面积之和为
项所占的格子的面积之和为![]() ,每段螺旋线与其所在的正方形所围成的扇形面积为
,每段螺旋线与其所在的正方形所围成的扇形面积为![]() ,则下列结论错误的是( )
,则下列结论错误的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个包装箱内有6件产品,其中4件正品,2件次品。现随机抽出两件产品.(要求罗列出所有的基本事件)
(1)求恰好有一件次品的概率。
(2)求都是正品的概率。
(3)求抽到次品的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com