
【题目】某高中为了解高中学生的性别和喜爱打篮球是否有关,对50名高中学生进行了问卷调查,得到如下列联表:
喜爱打篮球 | 不喜欢打篮球 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 |
已知在这50人中随机抽取1人,抽到喜欢打篮球的学生的概率为![]() .
.
(1)请将上述列联表补充完整;
(2)判断是否有99.5%的把握认为喜欢打篮球与性别有关?
附: 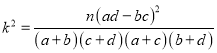
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,在以极点为直角坐标原点
,在以极点为直角坐标原点![]() ,极轴为
,极轴为![]() 轴的正半轴建立的平面直角坐标系
轴的正半轴建立的平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为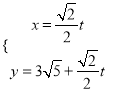 (
(![]() 为参数).
为参数).
(1)写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)在平面直角坐标系中,设曲线![]() 经过伸缩变换
经过伸缩变换![]() :
:  得到曲线
得到曲线![]() ,若
,若![]() 为曲线
为曲线![]() 上任意一点,求点
上任意一点,求点![]() 到直线
到直线![]() 的最小距离.
的最小距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次反恐演习中,我方三架武装直升机分别从不同方位对同一目标发动攻击(各发射一枚导弹),由于天气原因,三枚导弹命中目标的概率分别为0.9,0.9,0.8,若至少有两枚导弹命中目标方可将其摧毁,则目标被摧毁的概率为( )
A. 0.998 B. 0.046 C. 0.002 D. 0.954
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“DD共享单车”是为城市人群提供便捷经济、绿色低碳的环保出行方式,根据目前在三明市的投放量与使用的情况,有人作了抽样调查,抽取年龄在二十至五十岁的不同性别的骑行者,统计数据如下表所示:
男性 | 女性 | 合计 | |
20~35岁 |
| 40 | 100 |
36~50岁 | 40 |
| 90 |
合计 | 100 | 90 | 190 |
(1)求统计数据表中![]() 的值;
的值;
(2)假设用抽到的100名20~35岁年龄的骑行者作为样本估计全市的该年龄段男女使用“DD共享单车”情况,现从全市的该年龄段骑行者中随机抽取3人,求恰有一名女性的概率;
(3)根据以上列联表,判断使用“DD共享单车”的人群中,能否有![]() 的把握认为“性别”与“年龄”有关,并说明理由.
的把握认为“性别”与“年龄”有关,并说明理由.
参考数表:
|
|
|
|
|
|
|
|
|
|
参考公式: 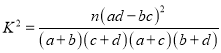 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司在迎新年晚会上举行抽奖活动,有甲、乙两个抽奖方案供员工选择;
方案甲:员工最多有两次抽奖机会,每次抽奖的中奖率为![]() .第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖,规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,获得奖金1000元;若未中奖,则所获奖金为0元.
.第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛一枚质地均匀的硬币,决定是否继续进行第二次抽奖,规定:若抛出硬币,反面朝上,员工则获得500元奖金,不进行第二次抽奖;若正面朝上,员工则须进行第二次抽奖,且在第二次抽奖中,若中奖,获得奖金1000元;若未中奖,则所获奖金为0元.
方案乙:员工连续三次抽奖,每次中奖率均为![]() ,每次中奖均可获奖金400元.
,每次中奖均可获奖金400元.
(1)求某员工选择方案甲进行抽奖所获奖金![]() (元)的分布列;
(元)的分布列;
(2)某员工选择方案乙与选择方案甲进行抽奖,试比较哪个方案更划算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(Ⅲ)当![]() 时,函数
时,函数![]() 在
在![]() 上的最大值为
上的最大值为![]() ,若存在
,若存在![]() ,使得
,使得![]() 成立,求实数b的取值范围.
成立,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,求曲线
,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在其定义域内为增函数,求
在其定义域内为增函数,求![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,设函数![]() ,若在
,若在![]() 上至少存在一点
上至少存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知菱形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于一点
相交于一点![]() ,
, ![]() ,将
,将![]() 沿着
沿着![]() 折起得
折起得![]() ,连接
,连接![]() .
.
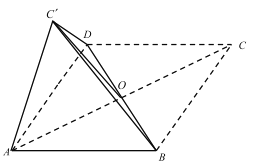
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若点![]() 在平面
在平面![]() 上的投影恰好是
上的投影恰好是![]() 的重心,求直线
的重心,求直线![]() 与底面
与底面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com