
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为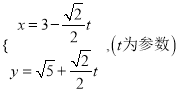 。在以原点
。在以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴的极坐标系中,圆
轴正半轴为极轴的极坐标系中,圆![]() 的方程为
的方程为![]() 。
。
(1)写出直线![]() 的普通方程和圆
的普通方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)若点P坐标为![]() ,圆
,圆![]() 与直线
与直线![]() 交于
交于![]() 两点,求
两点,求![]() 的值。
的值。
【答案】(1)![]()
![]() (2)
(2)![]()
【解答】解:(Ⅰ)由 得直线l的普通方程为x+y﹣3﹣
得直线l的普通方程为x+y﹣3﹣![]() =0
=0
又由![]() 得 ρ2=2
得 ρ2=2![]() ρsinθ,化为直角坐标方程为x2+(y﹣
ρsinθ,化为直角坐标方程为x2+(y﹣![]() )2=5;
)2=5;
(Ⅱ)把直线l的参数方程代入圆C的直角坐标方程,
得(3﹣![]() t)2+(
t)2+(![]() t)2=5,即t2﹣3
t)2=5,即t2﹣3![]() t+4=0
t+4=0
设t1,t2是上述方程的两实数根,
所以t1+t2=3![]()
又直线l过点P![]() ,A、B两点对应的参数分别为t1,t2,
,A、B两点对应的参数分别为t1,t2,
所以|PA|+|PB|=|t1|+|t2|=t1+t2=3![]() .
.
【解析】试题分析:(1)由加减消元得直线![]() 的普通方程,由
的普通方程,由![]() 得圆
得圆![]() 的直角坐标方程;(2)把直线l的参数方程代入圆C的直角坐标方程,由直线参数方程几何意义得|PA|+|PB|=|t1|+|t2|=t1+t2,再根据韦达定理可得结果
的直角坐标方程;(2)把直线l的参数方程代入圆C的直角坐标方程,由直线参数方程几何意义得|PA|+|PB|=|t1|+|t2|=t1+t2,再根据韦达定理可得结果
试题解析:解:(Ⅰ)由 得直线l的普通方程为x+y﹣3﹣
得直线l的普通方程为x+y﹣3﹣![]() =0
=0
又由![]() 得 ρ2=2
得 ρ2=2![]() ρsinθ,化为直角坐标方程为x2+(y﹣
ρsinθ,化为直角坐标方程为x2+(y﹣![]() )2=5;
)2=5;
(Ⅱ)把直线l的参数方程代入圆C的直角坐标方程,
得(3﹣![]() t)2+(
t)2+(![]() t)2=5,即t2﹣3
t)2=5,即t2﹣3![]() t+4=0
t+4=0
设t1,t2是上述方程的两实数根,
所以t1+t2=3![]()
又直线l过点P![]() ,A、B两点对应的参数分别为t1,t2,
,A、B两点对应的参数分别为t1,t2,
所以|PA|+|PB|=|t1|+|t2|=t1+t2=3![]() .
.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
【题目】为了解某校高三学生的视力情况,随机地抽查了该校1000名高三学生的视力情况,得到频率分布直方图,如图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为![]() ,视力在4.6到5.0之间的学生数
,视力在4.6到5.0之间的学生数![]() ,
, ![]() 的值分别为( )
的值分别为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在圆![]() 上任取一点
上任取一点![]() ,过点
,过点![]() 作
作![]() 轴的垂线段,
轴的垂线段, ![]() 为垂足,点
为垂足,点![]() 在线段
在线段![]() 上,且
上,且![]() ,点
,点![]() 在圆上运动。
在圆上运动。
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)过定点![]() 的直线与点
的直线与点![]() 的轨迹交于
的轨迹交于![]() 两点,在
两点,在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 为常数,若存在,求出点
为常数,若存在,求出点![]() 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面给出四种说法:
①用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好;
②命题P:“x0∈R,x02﹣x0﹣1>0”的否定是¬P:“x∈R,x2﹣x﹣1≤0”;
③设随机变量X服从正态分布N(0,1),若P(x>1)=p则P(﹣1<X<0)=![]() ﹣p
﹣p
④回归直线一定过样本点的中心(![]() ).
).
其中正确的说法有( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂商调查甲、乙两种不同型号电视机在10个卖场的销售量(单位:台),并根据这10个卖场的销售情况,得到如图所示的茎叶图.
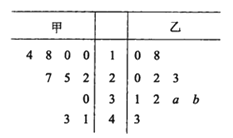
为了鼓励卖场,在同型号电视机的销售中,该厂商将销售量高于数据平均数的卖场命名为该型号电视机的“星级卖场”.
(1)当![]() 时,记甲型号电视机的“星级卖场”数量为
时,记甲型号电视机的“星级卖场”数量为![]() ,乙型号电视机的“星级卖场”数量为
,乙型号电视机的“星级卖场”数量为![]() ,比较
,比较![]() 的大小关系;
的大小关系;
(2)在这10个卖场中,随机选取2个卖场,记![]() 为其中甲型号电视机的“星级卖场”的个数,求
为其中甲型号电视机的“星级卖场”的个数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)若![]() ,记乙型号电视机销售量的方差为
,记乙型号电视机销售量的方差为![]() ,根据茎叶图推断
,根据茎叶图推断![]() 为何值时,
为何值时,![]() 达到最小值.(只需写出结论)
达到最小值.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高三(1)班班主任李老师为了了解本班学生喜爱中国古典文学是否与性别有关,对全班50人进行了问卷调查,得到如下列联表:
喜欢中国古典文学 | 不喜欢中国古典文学 | 合计 | |
女生 | 5 | ||
男生 | 10 | ||
合计 | 50 |
已知从全班50人中随机抽取1人,抽到喜欢中国古典文学的学生的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有![]() 的把握认为喜欢中国古典文学与性别有关?请说明理由;
的把握认为喜欢中国古典文学与性别有关?请说明理由;
(3)已知在喜欢中国古典文学的10位男生中,![]() ,
,![]() ,
,![]() 还喜欢数学,
还喜欢数学,![]() ,
,![]() 还喜欢绘画,
还喜欢绘画,![]() ,
,![]() 还喜欢体育.现从喜欢数学、绘画和体育的男生中各选出1名进行其他方面的调查,求
还喜欢体育.现从喜欢数学、绘画和体育的男生中各选出1名进行其他方面的调查,求![]() 和
和![]() 不全被选中的概率.
不全被选中的概率.
参考公式及数据:![]() ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com