
【题目】再直角坐标系中,定义两点![]() ,
,![]() 间的“直角距离”为
间的“直角距离”为![]() ,现有下列命题:
,现有下列命题:
①若![]() ,
,![]() 是
是![]() 轴上两点,则
轴上两点,则![]()
②已知![]() ,
,![]() ,则
,则![]() 为定值
为定值
③原点![]() 到直线
到直线![]() 上任一点
上任一点![]() 的直角距离
的直角距离![]() 的最小值为
的最小值为![]()
④设![]() 且
且![]() ,
,![]() ,若点
,若点![]() 是在过
是在过![]() 与
与![]() 的直线上,且点
的直线上,且点![]() 到点
到点![]() 与
与![]() 的“直角距离”之和等于
的“直角距离”之和等于![]() ,那么满足条件的点
,那么满足条件的点![]() 只有
只有![]() 个.
个.
其中的真命题是____________.(写出所有真命题的序号)
科目:高中数学 来源: 题型:
【题目】给出以下三个命题:
①若![]() ,则
,则![]() ;
;
②在![]() 中,若
中,若![]() ,则
,则![]() ;
;
③在一元二次方程![]() 中,若
中,若![]() ,则方程有实数根.
,则方程有实数根.
其中原命题、逆命题、否命题、逆否命题均为真命题的是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市政府为了节约生活用电,计划在本市试行居民生活用电定额管理,即确定一户居民月用电量标准a,用电量不超过a的部分按平价收费,超出a的部分按议价收费![]() 为此,政府调查了100户居民的月平均用电量
为此,政府调查了100户居民的月平均用电量![]() 单位:度
单位:度![]() ,以
,以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图所示.
分组的频率分布直方图如图所示.
![]() 根据频率分布直方图的数据,求直方图中x的值并估计该市每户居民月平均用电量
根据频率分布直方图的数据,求直方图中x的值并估计该市每户居民月平均用电量![]() 的值;
的值;
![]() 用频率估计概率,利用
用频率估计概率,利用![]() 的结果,假设该市每户居民月平均用电量X服从正态分布
的结果,假设该市每户居民月平均用电量X服从正态分布![]()
![]() 估计该市居民月平均用电量介于
估计该市居民月平均用电量介于![]() 度之间的概率;
度之间的概率;
![]() 利用
利用![]() 的结论,从该市所有居民中随机抽取3户,记月平均用电量介于
的结论,从该市所有居民中随机抽取3户,记月平均用电量介于![]() 度之间的户数为
度之间的户数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商家在某一天统计前5名顾客扫微信红包所得金额分别为5.9元,5.7元,4.7元,3.3元,2.1元,商家从这5名顾客中随机抽取3人赠送礼品.
(Ⅰ)求获得礼品的3人中恰好有2人的红包超过5元的概率;
(Ⅱ)商家统计一周内每天使用微信支付的人数![]() 与每天的净利润
与每天的净利润![]() (单位:元),得到如下表:
(单位:元),得到如下表:
| 12 | 16 | 22 | 25 | 26 | 29 | 30 |
| 60 | 100 | 210 | 240 | 150 | 270 | 330 |
根据表中数据用最小二乘法求![]() 与
与![]() 的回归方程
的回归方程![]() (
(![]() ,
,![]() 的计算结果精确到小数点后第二位)并估计使用微信支付的人数增加到36人时,商家当天的净利润为多少(计算结果精确到小数点后第二位)?
的计算结果精确到小数点后第二位)并估计使用微信支付的人数增加到36人时,商家当天的净利润为多少(计算结果精确到小数点后第二位)?
参考数据及公式:
①![]() ,
,![]() ;
;![]() ;
;![]()
②回归方程:![]() (其中
(其中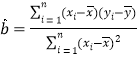 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在底面是菱形的四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .
.
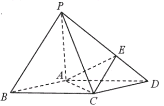
(1)证明:![]() 面
面![]() ;
;
(2)在棱![]() 上是否存在一点
上是否存在一点![]() ,使三棱锥
,使三棱锥![]() 是正三棱锥?证明你的结论.
是正三棱锥?证明你的结论.
(3)求以![]() 为棱,
为棱,![]() 与
与![]() 为面的二面角
为面的二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现采用随机模拟的方法估计某运动员射击4次,至少击中3次的概率:先由计算器给出0到9之间取整数值的随机数,指定0,1表示没有击中目标,2,3,4,5,6,7, 8,9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了 20组随机数:
7527 0293 7140 9857 0347 4373 8636 6947 1417 4698
0371 6233 2616 8045 6011 3661 9597 7424 7610 4281
根据以上数据估计该射击运动员射击4次至少击中3次的概率为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线![]() (其中
(其中![]() )的焦点
)的焦点![]() 的直线交抛物线于
的直线交抛物线于![]() 两点,且
两点,且![]() 两点的纵坐标之积为
两点的纵坐标之积为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)对于![]() 轴上给定的点
轴上给定的点![]() (其中
(其中![]() ),若过点
),若过点![]() 和
和![]() 两点的直线交抛物线
两点的直线交抛物线![]() 的准线
的准线![]() 点,求证:直线
点,求证:直线![]() 与
与![]() 轴交于一定点.
轴交于一定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在
是定义在![]() 上的奇函数,当
上的奇函数,当![]() 时,
时,![]() ,给出下列命题:
,给出下列命题:
①当![]() 时,
时,![]() ②函数
②函数![]() 有3个零点
有3个零点
③![]() 的解集为
的解集为![]() ④
④![]() ,都有
,都有![]()
其中正确命题的个数是( )
A. 4B. 3C. 2D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com