
【题目】已知平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是线段
是线段![]() 的中点,沿
的中点,沿![]() 将
将![]() 翻折到
翻折到![]() ,使得平面
,使得平面![]() 平面
平面![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
科目:高中数学 来源: 题型:
【题目】如图1所示,在等腰梯形ABCD中,![]() ,
,![]() ,垂足为E,
,垂足为E,![]() ,
,![]() 将
将![]() 沿EC折起到
沿EC折起到![]() 的位置,如图2所示,使平面
的位置,如图2所示,使平面![]() 平面ABCE.
平面ABCE.
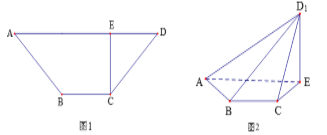
(1)连结BE,证明:![]() 平面
平面![]() ;
;
(2)在棱![]() 上是否存在点G,使得
上是否存在点G,使得![]() 平面
平面![]() ,若存在,直接指出点G的位置
,若存在,直接指出点G的位置![]() 不必说明理由
不必说明理由![]() ,并求出此时三棱锥
,并求出此时三棱锥![]() 的体积;若不存在,请说明理由.
的体积;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中曲线
中曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,直线
轴的正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程以及直线
的普通方程以及直线![]() 的直角坐标方程;
的直角坐标方程;
(2)将曲线![]() 向左平移2个单位,再将曲线
向左平移2个单位,再将曲线![]() 上的所有点的横坐标缩短为原来的
上的所有点的横坐标缩短为原来的![]() ,得到曲线
,得到曲线![]() ,求曲线
,求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题10分)选修4—4:坐标系与参数方程
已知曲线C1的参数方程为![]() (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ。
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ。
(Ⅰ)把C1的参数方程化为极坐标方程;
(Ⅱ)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣1|+|2x﹣6|(x∈R),记f(x)的最小值为c.
(1)求c的值;
(2)若实数ab满足a>0,b>0,a+b=c,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设各项均为正数的数列{an}的前n项和为Sn,已知a1=1,且anSn+1﹣an+1Sn=an+1﹣λan,对一切n∈N*都成立.
(1)当λ=1时;
①求数列{an}的通项公式;
②若bn=(n+1)an,求数列{bn}的前n项的和Tn;
(2)是否存在实数λ,使数列{an}是等差数列如果存在,求出λ的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com