
【题目】已知数列{an}的首项![]() (a是常数),
(a是常数),![]() (
(![]() ).
).
(1)求![]() ,
,![]() ,
,![]() ,并判断是否存在实数a使
,并判断是否存在实数a使![]() 成等差数列.若存在,求出
成等差数列.若存在,求出![]() 的通项公式;若不存在,说明理由;
的通项公式;若不存在,说明理由;
(2)设![]() ,
,![]() (
(![]() ),
),![]() 为数列
为数列![]() 的前n项和,求
的前n项和,求![]()
科目:高中数学 来源: 题型:
【题目】一位同学家里订了一份报纸,送报人每天都在早上6 : 207 : 40之间将报纸送达,该同学需要早上7 : 008 : 00之间出发上学,则这位同学在离开家之前能拿到报纸的概率为 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位将举办庆典活动,要在广场上竖立一形状为等腰梯形的彩门BADC (如图),设计要求彩门的面积为S (单位:m2)高为h(单位:m)(S,h为常数),彩门的下底BC固定在广场地面上,上底和两腰由不锈钢支架构成,设腰和下底的夹角为α,不锈钢支架的长度和记为l. 
(1)请将l表示成关于α的函数l=f(α);
(2)问当α为何值时l最小?并求最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某几何体的三视图如图所示,P是正方形ABCD对角线的交点,G是PB的中点.
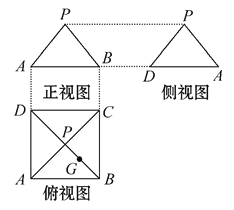
(1)根据三视图,画出该几何体的直观图.
(2)在直观图中,①证明:PD∥平面AGC;
②证明:平面PBD⊥平面AGC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 、
、![]() 为椭圆
为椭圆![]() :
: ![]() (
(![]() )的左、右焦点,点
)的左、右焦点,点![]() 为椭圆上一点,且
为椭圆上一点,且![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若圆![]() 是以
是以![]() 为直径的圆,直线
为直径的圆,直线![]() :
: ![]() 与圆
与圆![]() 相切,并与椭圆
相切,并与椭圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某几何体的三视图如图所示,P是正方形ABCD对角线的交点,G是PB的中点.
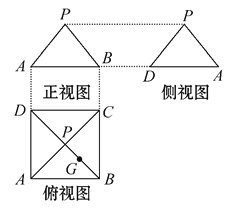
(1)根据三视图,画出该几何体的直观图.
(2)在直观图中,①证明:PD∥平面AGC;
②证明:平面PBD⊥平面AGC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两圆![]() ,
, ![]() 的圆心分别为c1,c2,,P为一个动点,且
的圆心分别为c1,c2,,P为一个动点,且![]() .
.
(1)求动点P的轨迹方程;
(2)是否存在过点A(2,0)的直线l与轨迹M交于不同的两点C,D,使得C1C=C1D?若存在,求出直线l的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com