
【题目】从甲、乙两名运动员的若干次训练成绩中随机抽取6次,分别为
甲:7.7,7.8,8.1,8.6,9.3,9.5
乙:7.6,8.0,8.2,8.5,9.2,9.5
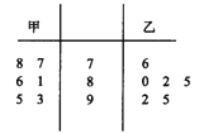
(1)根据以上的茎叶图,不用计算说一下甲乙谁的方差大,并说明谁的成绩稳定;
(2)从甲、乙运动员高于8.1分成绩中各随机抽取1次成绩,求甲、乙运动员的成绩至少有一个高于9.2分的概率.
(3)经过对甲、乙运动员若干次成绩进行统计,发现甲运动员成绩均匀分布在[7.5,9.5]之间,乙运动员成绩均匀分布在[7.0,10]之间,现甲、乙比赛一次,求甲、乙成绩之差的绝对值小于0.5分的概率.
【答案】(1)甲方差大,乙方差小,乙稳定(2)![]() (3)
(3)![]()
【解析】
(1)根据茎叶图,结合甲乙两名运动员的成绩集中与分散程度,看出两个人的方差(或标准差),从而比较出两个人发挥的稳定性;(2)利用古典概型概率公式求出满足甲、乙运动员的成绩都不高于![]() 分的概型,利用对立事件的概率公式即可求出结果;(3)根据已知中甲运动员成绩均匀分布在
分的概型,利用对立事件的概率公式即可求出结果;(3)根据已知中甲运动员成绩均匀分布在![]() 之间,乙运动员成绩均匀分布在
之间,乙运动员成绩均匀分布在![]() 之间,我们可以求出它所表示的平面区域的面积,再求出甲、乙成绩之差的绝对值小于
之间,我们可以求出它所表示的平面区域的面积,再求出甲、乙成绩之差的绝对值小于![]() 分对应的平面区域的面积,代入几何概型公式,即可得到结果.
分对应的平面区域的面积,代入几何概型公式,即可得到结果.
(1)甲方差大,乙方差小,乙稳定
(2)设甲乙成绩至少有一个高于9.2分为事件 ![]() ,则
,则
![]()
(3)设甲运动员成绩为 ![]() ,则
,则 ![]() 乙运动员成绩为
乙运动员成绩为 ![]() ,
, ![]()
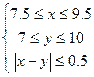
设甲乙运动员成绩之差的绝对值小于 ![]() 的事件为
的事件为 ![]() ,则
,则


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是等边三角形. 
(1)证明:PB⊥CD;
(2)求二面角A﹣PD﹣C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=  ,若存在实数x1 , x2 , x3 , x4满足f(xl)=f(x2)=f(x3)=f(x4),且x1<x2<x3<x4 , 则x1x2x3x4的取值范围是
,若存在实数x1 , x2 , x3 , x4满足f(xl)=f(x2)=f(x3)=f(x4),且x1<x2<x3<x4 , 则x1x2x3x4的取值范围是
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的奇函数f(x)和偶函数g(x)满足f(x)+g(x)=ax﹣a﹣x+2,若g(2)=a,则f(2)=( )
A.2
B.![]()
C.![]()
D.a2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx﹣ax﹣3(a≠0).
(1)讨论f(x)的单调性;
(2)若f(x)+(a+1)x+4﹣e≤0对任意x∈[e,e2]恒成立,求实数a的取值范围(e为自然常数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且Sn=n2+n.
(1)求数列{an}的通项公式an;
(2)数列{bn}满足bn= ![]() (n∈N*),求数列{bn}的前n项和Tn .
(n∈N*),求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲罐中有3个红球,2个白球和3个黑球,乙罐中有5个红球,3个白球和3个黑球.先从甲罐中随机取出一球放入乙罐,分别以![]() ,
,![]() 和
和![]() 表示由甲罐取出的球是红球,白球和黑球的事件;再从乙罐中随机取出一球,以
表示由甲罐取出的球是红球,白球和黑球的事件;再从乙罐中随机取出一球,以![]() 表示由乙罐取出的球是红球的事件,则下列结论中正确的是__________(写出所有正确结论的序号).
表示由乙罐取出的球是红球的事件,则下列结论中正确的是__________(写出所有正确结论的序号).
①P(B)=![]() ;②
;②![]() ;
;
③事件B与事件A1相互独立;
④A1,A2,A3是两两互斥的事件;
⑤P(B)的值不能确定,因为它与A1,A2,A3中究竟哪一个发生有关.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在对人们休闲方式的一次调查中,其中主要休闲方式的选择有看电视和运动,现共调查了100人,已知在这100人中随机抽取1人,抽到主要休闲方式为看电视的人的概率为![]() 。
。
(1)完成下列2×2列联表;
休闲方式为看电视 | 休闲方式为运动 | 合计 | |
女性 | 40 | ||
男性 | 30 | ||
合计 |
(2)请判断是否可以在犯错误的概率不超过0.005的前提下认为性别与休闲方式有关系?
参考公式![]()
P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.025 | 0.010 | 0.005 |
k | 1.323 | 2.072 | 2.706 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCDA1B1C1D1中,O为底面ABCD的中心,P,Q分别为![]() 的中点.
的中点.
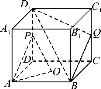
求证:(1)平面D1 BQ∥平面PAO.
(2)求异面直线QD1与AO所成角的余弦值;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com