
【题目】在平面直角坐标系中,点集A={(x,y)|x2+y2≤1},B={(x,y)|x≤4,y≥0,3x﹣4y≥0},则点集Q={(x,y)|x=x1+x2,y=y1+y2,(x1,y1)∈A,(x2,y2)∈B}所表示的区域的面积为_____.
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,若acos2![]() +ccos2
+ccos2![]() =
=![]() b.
b.
(1)求证:a,b,c成等差数列;
(2)若∠B=60°,b=4,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解一种植物果实的情况,随机抽取一批该植物果实样本测量重量(单位:克),按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分为5组,其频率分布直方图如图所示.
分为5组,其频率分布直方图如图所示.
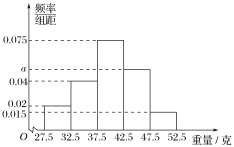
(1)求图中![]() 的值;
的值;
(2)估计这种植物果实重量的平均数![]() 和方差
和方差![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(3)已知这种植物果实重量不低于32.5克的即为优质果实,用样本估计总体.若从这种植物果实中随机抽取3个,其中优质果实的个数为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(2)若直线![]() 是函数
是函数![]() 图象的切线,求
图象的切线,求![]() 的最小值;
的最小值;
(3)当![]() 时,若直线
时,若直线![]() 是函数
是函数![]() 图象有两个交点,求实数
图象有两个交点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三共有1000位学生,为了分析某次的数学考试成绩,采取随机抽样的方法抽取了50位高三学生的成绩进行统计分析,得到如图所示频数分布表:
分组 |
|
|
|
|
|
频数 | 3 | 11 | 18 | 12 | 6 |
(1)根据频数分布表计算成绩在![]() 的频率并计算这组数据的平均值
的频率并计算这组数据的平均值![]() (同组的数据用该组区间的中点值代替);
(同组的数据用该组区间的中点值代替);
(2)用分层抽样的方法从成绩在![]() 和
和![]() 的学生中共抽取5人,从这5人中任取2人,求成绩在
的学生中共抽取5人,从这5人中任取2人,求成绩在![]() 和
和![]() 中各有1人的概率.
中各有1人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生物探测器在水中逆流行进时,所消耗的能量为E=cvnT,其中v为行进时相对于水的速度,T为行进时的时间(单位:h),c为常数,n为能量次级数,如果水的速度为4km/h,该生物探测器在水中逆流行进200km.
(1)求T关于v的函数关系式;
(2)①当能量次级数为2时,求探测器消耗的最少能量;
②当能量次级数为3时,试确定v的大小,使该探测器消耗的能量最少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=exsinx,g(x)为f(x)的导函数,
(1)求f(x)的单调区间;
(2)当x∈[![]() ,π],证明:f(x)+g(x)(π﹣x)≥0.
,π],证明:f(x)+g(x)(π﹣x)≥0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人沿固定路线开车上班,沿途共有![]() 个红绿灯,他对过去
个红绿灯,他对过去![]() 个工作日上班途中的路况进行了统计,得到了如表的数据:
个工作日上班途中的路况进行了统计,得到了如表的数据:
上班路上遇见的红灯数 |
|
|
|
|
|
|
天数 |
|
|
|
|
|
|
若一路绿灯,则他从家到达公司只需用时![]() 分钟,每遇一个红灯,则会多耗时
分钟,每遇一个红灯,则会多耗时![]() 分钟,以频率作为概率的估计值
分钟,以频率作为概率的估计值
(1)试估计他平均每天上班需要用时多少分钟?
(2)若想以不少于![]() 的概率在早上
的概率在早上![]() 点前(含
点前(含![]() 点)到达公司,他最晚何时要离家去公司?
点)到达公司,他最晚何时要离家去公司?
(3)公司规定,员工应早上![]() 点(含
点(含![]() 点)前打卡考勤,否则视为迟到,每迟到一次,会被罚款
点)前打卡考勤,否则视为迟到,每迟到一次,会被罚款![]() 元.因某些客观原因,在接下来的
元.因某些客观原因,在接下来的![]() 个工作日里,他每天早上只能
个工作日里,他每天早上只能![]() 从家出发去公司,求他因迟到而被罚款的期望.
从家出发去公司,求他因迟到而被罚款的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中.直线1的参数方程为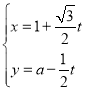 (t为参数).在以坐标原点为极点,x轴的非负半轴为极轴的极坐标系中.曲线C的极坐标方程为ρ=2cosθ.
(t为参数).在以坐标原点为极点,x轴的非负半轴为极轴的极坐标系中.曲线C的极坐标方程为ρ=2cosθ.
(1)若曲线C关于直线l对称,求a的值;
(2)若A、B为曲线C上两点.且∠AOB![]() ,求|OA|+|OB|的最大值.
,求|OA|+|OB|的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com