
| A. | (-∞,-4) | B. | [-4,-3] | C. | (-4,-3] | D. | [-3,+∞) |
分析 作出函数$f(x)=\left\{\begin{array}{l}{x^2}+2x-3,x≤0\\ lnx-a,x>0\end{array}\right.({a∈R})$的图象,结合图象,能求出实数k的取值范围.
解答 解:作出函数$f(x)=\left\{\begin{array}{l}{x^2}+2x-3,x≤0\\ lnx-a,x>0\end{array}\right.({a∈R})$的图象,如下图: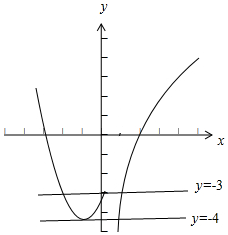
∵关于x的方程f(x)=k有三个不等的实根,
∴函数$f(x)=\left\{\begin{array}{l}{x^2}+2x-3,x≤0\\ lnx-a,x>0\end{array}\right.({a∈R})$的图象与直线y=k在三个不同的交点,
结合图象,得:-4<k≤-3.
∴实数k的取值范围是(-4,-3].
故选C.
点评 本题考查实数的取值范围的求法,是基础题,解题时要认真审题,注意数形结合思想的合理运用.


 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
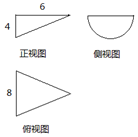 某几何体的三视图是如图所示的直角三角形、半圆和等腰三角形,各边的长度如图所示,则此几何体的体积是16π,表面积是$24+(8+4\sqrt{13})π$.
某几何体的三视图是如图所示的直角三角形、半圆和等腰三角形,各边的长度如图所示,则此几何体的体积是16π,表面积是$24+(8+4\sqrt{13})π$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥中P-ABCD,AB=BC=CD=DA,∠BAD=60°,AQ=QD,△PAD是正三角形.
如图,在四棱锥中P-ABCD,AB=BC=CD=DA,∠BAD=60°,AQ=QD,△PAD是正三角形.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\frac{1}{x}$ | B. | y=x2 | C. | y=($\frac{1}{2}$)x | D. | y=$\frac{1}{{x}^{2}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com