
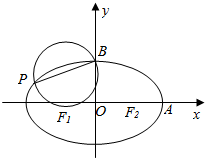
 设椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点为F1,F2,右顶点为A,上顶点为B.已知|AB|=$\frac{\sqrt{3}}{2}$|F1F2|.
设椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点为F1,F2,右顶点为A,上顶点为B.已知|AB|=$\frac{\sqrt{3}}{2}$|F1F2|.分析 (1)设椭圆的右焦点为F2(c,0),由|AB|=$\frac{\sqrt{3}}{2}$|F1F2|.可得$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{3}$c,再利用b2=a2-c2,e=$\frac{c}{a}$即可得出;
(2)由(1)可得b2=c2.可设椭圆方程为$\frac{{x}^{2}}{2{c}^{2}}$+$\frac{{y}^{2}}{{c}^{2}}$=1,设P(x0,y0),由F1(-c,0),B(0,c),可得$\overrightarrow{{F}_{1}P}$,$\overrightarrow{{F}_{1}B}$.利用圆的性质可得$\overrightarrow{{F}_{1}B}$⊥$\overrightarrow{{F}_{1}P}$,于是$\overrightarrow{{F}_{1}B}$•$\overrightarrow{{F}_{1}P}$=0,得到x0+y0+c=0,由于点P在椭圆上,可得$\frac{{{x}_{0}}^{2}}{2{c}^{2}}$+$\frac{{{y}_{0}}^{2}}{{c}^{2}}$=1.联立可得3x02+4cx0=0,解得P(-$\frac{4}{3}$c,$\frac{1}{3}$c).设圆心为T(x1,y1),利用中点坐标公式可得T(-$\frac{2}{3}$c,$\frac{2}{3}$c),利用两点间的距离公式可得圆的半径r.设直线l的方程为:y=kx.利用直线与圆相切的性质即可得出.
解答 解:(1)设椭圆的右焦点F2的坐标为(c,0).
由$|{AB}|=\frac{{\sqrt{3}}}{2}|{{F_1}{F_2}}|$,可得a2+b2=3c2,又b2=a2-c2,则$\frac{c^2}{a^2}=\frac{1}{2}$.
所以,椭圆的离心率$e=\frac{{\sqrt{2}}}{2}$.$\sqrt{{a^2}+{b^2}}=\sqrt{3}c$,
所以2a2-c2=3c2,解得$a=\sqrt{2}c$,$e=\frac{{\sqrt{2}}}{2}$;
(2)假设存在经过原点的直线l与该圆相切,由(1)知a2=2c2,b2=c2.
故椭圆方程为$\frac{x^2}{{2{c^2}}}+\frac{y^2}{c^2}=1$.
设P(x0,y0).由F1(-c,0),B(0,c),
有$\overrightarrow{{F_1}P}=({{x_0}+c,{y_0}})$,$\overrightarrow{{F_1}B}=({c,c})$.由已知,有$\overrightarrow{{F_1}P}•\overrightarrow{{F_1}B}=0$,
即(x0+c)c+y0c=0.又c≠0,故有x0+y0+c=0.①
又因为点P在椭圆上,故$\frac{{{x_0}^2}}{{2{c^2}}}+\frac{{{y_0}^2}}{c^2}=1$.②
由①和②可得$3{x_0}^2+4c{x_0}=0$.而点P不是椭圆的顶点,
故${x_0}=-\frac{4c}{3}$,代入①得${y_0}=\frac{c}{3}$,即点P的坐标为$({-\frac{4c}{3},\frac{c}{3}})$.
设圆的圆心为T(x1,y1),则${x_1}=\frac{{-\frac{4}{3}c+0}}{2}=-\frac{2}{3}c$,${y_1}=\frac{{\frac{c}{3}+c}}{2}=\frac{2}{3}c$,
进而圆的半径$r=\sqrt{{{({{x_1}-0})}^2}+{{({{y_1}-c})}^2}}=\frac{{\sqrt{5}}}{3}c$.
(ⅰ)直线l的斜率不存在时,l:x=0,此时$d=\frac{2}{3}c≠r$,不合题意;
(ⅱ)直线l的斜率不存在时,设l的斜率为k,依题意,直线l的方程为y=kx.
由l与圆相切,可得$\frac{{|{k{x_1}-{y_1}}|}}{{\sqrt{{k^2}+1}}}=r$,即$\frac{{|{k({-\frac{2c}{3}})-\frac{2c}{3}}|}}{{\sqrt{{k^2}+1}}}=\frac{{\sqrt{5}}}{3}c$,
整理得k2-8k+1=0,解得$k=4±\sqrt{15}$,$l:y=({4±\sqrt{15}})x$.
综上,存在符合条件的直线,方程为$l:y=({4±\sqrt{15}})x$.
点评 本题中考查了椭圆与圆的标准方程及其性质、点与椭圆的位置关系、直线与圆相切问题、点到直线的距离公式、中点坐标公式等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
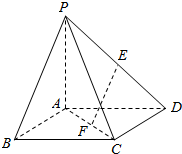 如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AD=1,E、F分别为PD、AC上的动点,且$\frac{DE}{DP}$=$\frac{CF}{CA}$=λ(0<λ<1).
如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AD=1,E、F分别为PD、AC上的动点,且$\frac{DE}{DP}$=$\frac{CF}{CA}$=λ(0<λ<1).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
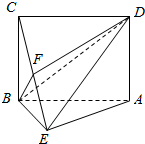 已知如图:四边形ABCD是矩形,BC⊥平面ABE,且AE=EB=BC=2,点F为CE上一点,且BF⊥平面ACE.
已知如图:四边形ABCD是矩形,BC⊥平面ABE,且AE=EB=BC=2,点F为CE上一点,且BF⊥平面ACE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
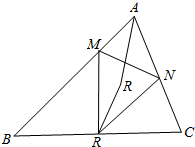 已知△ABC为锐角三角形,AB≠AC,以BC为直径的圆分别交边AB和AC于点M和N,记BC得中点为O,∠BAC的平分线和∠MON的平分线交于点R.证明:△BMR的外接圆和△CNR的外接圆有一个交点在BC上.
已知△ABC为锐角三角形,AB≠AC,以BC为直径的圆分别交边AB和AC于点M和N,记BC得中点为O,∠BAC的平分线和∠MON的平分线交于点R.证明:△BMR的外接圆和△CNR的外接圆有一个交点在BC上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com