
【题目】下列说法正确的个数是( ) ①命题“x∈R,x3﹣x2+1≤0”的否定是“ ![]() ;
;
②“ ![]() ”是“三个数a,b,c成等比数列”的充要条件;
”是“三个数a,b,c成等比数列”的充要条件;
③“m=﹣1”是“直线mx+(2m﹣1)y+1=0和直线3x+my+2=0垂直”的充要条件:
A.0
B.1
C.2
D.3
【答案】B
【解析】解:①命题“x∈R,x3﹣x2+1≤0”的否定是“x0∈R, ![]() >0,故①正确; ②由
>0,故①正确; ②由 ![]() ,不一定有a,b,c成等比数列,如a=0,b=0,c=1,
,不一定有a,b,c成等比数列,如a=0,b=0,c=1,
反之,三个数a,b,c成等比数列,不一定有 ![]() ,如a=1,b=﹣2,c=4.
,如a=1,b=﹣2,c=4.
∴“ ![]() ”是“三个数a,b,c成等比数列”的既不充分也不必要的条件,故②错误;
”是“三个数a,b,c成等比数列”的既不充分也不必要的条件,故②错误;
③当m=﹣1时,两直线分别化为﹣x﹣3y+1=0和3x﹣y+2=0,两直线垂直,
反之,由两直线垂直,得3m+m(2m﹣1)=0,解得m=0或m=﹣1.
∴“m=﹣1”是“直线mx+(2m﹣1)y+1=0和直线3x+my+2=0垂直”的充分不必要条件,故③错误.
∴正确的命题个数是1个.
故选:B.
【考点精析】通过灵活运用命题的真假判断与应用,掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系即可以解答此题.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两人约定晚6点到晚7点之间在某处见面,并约定甲若早到应等乙半小时,而乙还有其他安排,若乙早到则不需等待,则甲、乙两人能见面的概率( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O为坐标原点,F是双曲线 ![]() 的左焦点,A,B分别为Γ的左、右顶点,P为Γ上一点,且PF⊥x轴,过点A的直线l与线段PF交于点M,与y轴交于点E,直线 BM与y轴交于点N,若|OE|=2|ON|,则 Γ的离心率为( )
的左焦点,A,B分别为Γ的左、右顶点,P为Γ上一点,且PF⊥x轴,过点A的直线l与线段PF交于点M,与y轴交于点E,直线 BM与y轴交于点N,若|OE|=2|ON|,则 Γ的离心率为( )
A.3
B.2
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆Γ: ![]() +y2=1(a>1)的左焦点为F1 , 右顶点为A1 , 上顶点为B1 , 过F1 , A1 , B1三点的圆P的圆心坐标为(
+y2=1(a>1)的左焦点为F1 , 右顶点为A1 , 上顶点为B1 , 过F1 , A1 , B1三点的圆P的圆心坐标为( ![]() ,
, ![]() ).
).
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线l:y=kx+m(k,m为常数,k≠0)与椭圆Γ交于不同的两点M和N.
(i)当直线l过E(1,0),且 ![]() +2
+2 ![]() =
= ![]() 时,求直线l的方程;
时,求直线l的方程;
(ii)当坐标原点O到直线l的距离为 ![]() 时,求△MON面积的最大值.
时,求△MON面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,CA=CB=AA1 , ∠BAA1=∠BAC=60°,点O是线段AB的中点. (Ⅰ)证明:BC1∥平面OA1C;
(Ⅱ)若AB=2,A1C= ![]() ,求二面角A﹣BC﹣A1的余弦值.
,求二面角A﹣BC﹣A1的余弦值.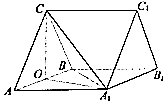
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且a1=2,nan+1=2(n+1)an
(1)记bn= ![]() ,求数列{bn}的通项bn;
,求数列{bn}的通项bn;
(2)求通项an及前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若F1 , F2是椭圆C: ![]() +
+ ![]() =1(0<m<9)的两个焦点,椭圆上存在一点P,满足以椭圆短轴为直径的圆与线段PF1相切于该线段的中点M. (Ⅰ)求椭圆C的方程;
=1(0<m<9)的两个焦点,椭圆上存在一点P,满足以椭圆短轴为直径的圆与线段PF1相切于该线段的中点M. (Ⅰ)求椭圆C的方程;
(Ⅱ)过点(0, ![]() )的直线l与椭圆C交于两点A、B,线段AB的中垂线l1交x轴于点N,R是线段AN的中点,求直线l1与直线BR的交点E的轨迹方程.
)的直线l与椭圆C交于两点A、B,线段AB的中垂线l1交x轴于点N,R是线段AN的中点,求直线l1与直线BR的交点E的轨迹方程.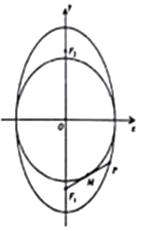
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com