
已知椭圆 (a>b>0)的左焦为F,右顶点为A,上顶点为B,O为坐标原点,M为椭圆上任意一点,过F,B,A三点的圆的圆心为(p,q).
(a>b>0)的左焦为F,右顶点为A,上顶点为B,O为坐标原点,M为椭圆上任意一点,过F,B,A三点的圆的圆心为(p,q).
(1).当p+q≤0时,求椭圆的离心率的取值范围;
(2).若D(b+1,0),在(1)的条件下,当椭圆的离心率最小时, 的最小值为
的最小值为 ,求椭圆的方程.
,求椭圆的方程.
(1)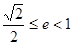 ;(2)
;(2)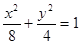 .
.
解析试题分析:本题主要考查直线和圆的方程、椭圆的方程、离心率、向量的运算、二次函数的最值等基础知识,意在考查考生的运算求解能力、推理论证能力以及利用函数与方程思想、数形结合思想的解题能力.
第一问,利用AF、AB的中垂线的交点为圆心,得到圆心坐标,由已知令 ,解出a,c的关系,从而求离心率e的范围;第二问,结合第一问得
,解出a,c的关系,从而求离心率e的范围;第二问,结合第一问得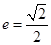 ,则得出基本量a,b,c的关系,设出椭圆方程,用c表示,并确定点M的横坐标的取值范围,利用向量的数量积,得出关于x的表达式,利用配方法,通过讨论抛物线的对称轴
,则得出基本量a,b,c的关系,设出椭圆方程,用c表示,并确定点M的横坐标的取值范围,利用向量的数量积,得出关于x的表达式,利用配方法,通过讨论抛物线的对称轴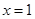 与
与 的大小来决定最小值在哪个位置取得,令最小值等于
的大小来决定最小值在哪个位置取得,令最小值等于 ,解出c的值,从而确定椭圆的标准方程.
,解出c的值,从而确定椭圆的标准方程.
试题解析:(1)设半焦距为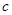 .由题意
.由题意 的中垂线方程分别为
的中垂线方程分别为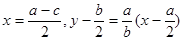 ,
,
于是圆心坐标为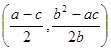 .所以
.所以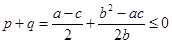 ,
,
整理得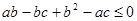 , 4分
, 4分
即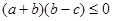 ,
,
所以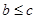 ,于是
,于是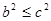 ,即
,即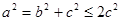 .
.
所以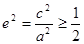 ,即
,即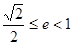 . 6分
. 6分
(2)当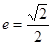 时,
时,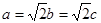 ,此时椭圆的方程为
,此时椭圆的方程为 ,
,
设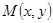 ,则
,则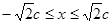 ,
,
所以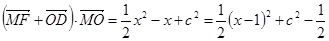 . 8分
. 8分
当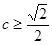 时,上式的最小值为
时,上式的最小值为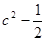 ,即
,即 ,得
,得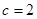 ; 10分
; 10分
当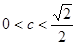 时,上式的最小值为
时,上式的最小值为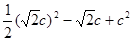 ,即
,即 ,
,
解得 ,不合题意,舍去.
,不合题意,舍去.
综上所述,椭圆的方程为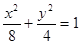 . 12分
. 12分
考点:直线和圆的方程、椭圆的方程、离心率、向量的运算、二次函数的最值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
某幼儿园准备建一个转盘,转盘的外围是一个周长为k米的圆.在这个圆上安装座位,且每个座位和圆心处的支点都有一根直的钢管相连经预算,转盘上的每个座位与支点相连的钢管的费用为3k元/根,且当两相邻的座位之间的圆弧长为x米时,相邻两座位之间的钢管和其中一个座位的总费用为 k元.假设座位等距分布,且至少有两个座位,所有座位都视为点,且不考虑其他因素,记转盘的总造价为y元.
k元.假设座位等距分布,且至少有两个座位,所有座位都视为点,且不考虑其他因素,记转盘的总造价为y元.
(1)试写出y关于x的函数关系式,并写出定义域;
(2)当k=50米时,试确定座位的个数,使得总造价最低?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设V为全体平面向量构成的集合,若映射f:
V→R满足:
对任意向量a=(x1,y1)∈V,b=(x2,y2)∈V,以及任意λ∈R,均有f[λa+(1-λ)b]=λf(a)+(1-λ)f(b),则称映射f具有性质p.
现给出如下映射:
①f1:V→R,f1(m)=x-y,m=(x,y)∈V;
②f2:V→R,f2(m)=x2+y,m=(x,y)∈V;
③f3:V→R,f3(m)=x+y+1,m=(x,y)∈V.
分析映射①②③是否具有性质p.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com