
【题目】![]() 年新型冠状病毒疫情爆发,贵州省教育厅号召全体学生“停课不停学”.自
年新型冠状病毒疫情爆发,贵州省教育厅号召全体学生“停课不停学”.自![]() 月
月![]() 日起,高三年级学生通过收看“阳光校园·空中黔课”进行线上网络学习.为了检测线上网络学习效果,某中学随机抽取
日起,高三年级学生通过收看“阳光校园·空中黔课”进行线上网络学习.为了检测线上网络学习效果,某中学随机抽取![]() 名高三年级学生做“是否准时提交作业”的问卷调查,并组织了一场线上测试,调查发现有
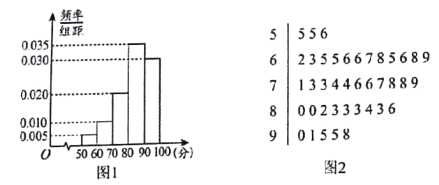
名高三年级学生做“是否准时提交作业”的问卷调查,并组织了一场线上测试,调查发现有![]() 名学生每天准时提交作业,根据他们的线上测试成绩得频率分布直方图(如图
名学生每天准时提交作业,根据他们的线上测试成绩得频率分布直方图(如图![]() 所示);另外
所示);另外![]() 名学生偶尔没有准时提交作业,根据他们的线上测试成绩得茎叶图(如图
名学生偶尔没有准时提交作业,根据他们的线上测试成绩得茎叶图(如图![]() 所示,单位:分)
所示,单位:分)
(1)成绩不低于![]() 分为
分为![]() 等,低于
等,低于![]() 分为非
分为非![]() 等.完成以下列联表,并判断是否有
等.完成以下列联表,并判断是否有![]() 以上的把握认为成绩取得
以上的把握认为成绩取得![]() 等与每天准时提交作业有关?
等与每天准时提交作业有关?
准时提交作业与成绩等次列联表 | 单位:人 | ||
A等 | 非A等 | 合计 | |
每天准时提交作业 | |||
偶尔没有准时提交作业 | |||
合计 | |||
(2)成绩低于![]() 分为不合格,从这
分为不合格,从这![]() 名学生里成绩不合格的学生中再抽取
名学生里成绩不合格的学生中再抽取![]() 人,其中每天准时提交作业的学生人数为
人,其中每天准时提交作业的学生人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
附: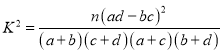
|
|
|
|
|
|
|
|
|
|
【答案】(1)列联表见解析,有![]() 以上的把握认为成绩取得
以上的把握认为成绩取得![]() 等与每天准时提交作业有关.(2)分布列见解析,
等与每天准时提交作业有关.(2)分布列见解析,![]() .
.
【解析】
(1)根据频率分布直方图计算出每天准时提交作业的![]() 等学生人数,再结合茎叶图中的数据可得出
等学生人数,再结合茎叶图中的数据可得出![]() 列联表,可计算出
列联表,可计算出![]() 的观测值,利用临界值表可得出结论;
的观测值,利用临界值表可得出结论;
(2)由频率分布直方图和茎叶图可知成绩低于![]() 分的学生共
分的学生共![]() 人,其中每天准时提交作业的有
人,其中每天准时提交作业的有![]() 人,偶尔没有准时提交作业的有
人,偶尔没有准时提交作业的有![]() 人,可知随机变量
人,可知随机变量![]() 的可能取值有
的可能取值有![]() 、
、![]() 、
、![]() 、
、![]() ,计算出随机变量
,计算出随机变量![]() 在不同取值下的概率,可得出随机变量
在不同取值下的概率,可得出随机变量![]() 的分布列,利用期望公式可计算出随机变量
的分布列,利用期望公式可计算出随机变量![]() 的数学期望值.
的数学期望值.
(1)每天准时提交作业的![]() 等学生人数为
等学生人数为![]() ,
,
根据题意得到列联表
A等 | 非A等 | 合计 | |
每天准时提交作业 |
|
|
|
偶尔没有准时提交作业 |
|
|
|
合计 |
|
|
|
![]() ,
,
所以有![]() 以上的把握认为成绩取得
以上的把握认为成绩取得![]() 等与每天准时提交作业有关;
等与每天准时提交作业有关;
(2)成绩低于![]() 分的学生共
分的学生共![]() 人,其中每天准时提交作业的有
人,其中每天准时提交作业的有![]() 人,偶尔没有准时提交作业的有
人,偶尔没有准时提交作业的有![]() 人,所以随机变量
人,所以随机变量![]() 的可能取值有
的可能取值有![]() 、
、![]() 、
、![]() 、
、![]() .
.
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
随机变量![]() 的分布列为:
的分布列为:
|
|
|
|
|
|
|
|
|
|
随机变量![]() 的数学期望为
的数学期望为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两人进行象棋比赛,采取五局三胜制(不考虑平局,先赢得三场的人为获胜者,比赛结束).根据前期的统计分析,得到甲在和乙的第一场比赛中,取胜的概率为0.5,受心理方面的影响,前一场比赛结果会对甲的下一场比赛产生影响,如果甲在某一场比赛中取胜,则下一场取胜率提高0.1,反之,降低0.1.则甲以3:1取得胜利的概率为( )
A.0.162B.0.18C.0.168D.0.174
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,设点
,设点![]() 为圆
为圆![]() 与
与![]() 轴负半轴的交点,点
轴负半轴的交点,点![]() 为圆
为圆![]() 上一点,且满足
上一点,且满足![]() 的中点在
的中点在![]() 轴上.
轴上.
(1)当![]() 变化时,求点
变化时,求点![]() 的轨迹方程;
的轨迹方程;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,
,![]() 、
、![]() 为曲线
为曲线![]() 上两个不同的点,且在
上两个不同的点,且在![]() 、
、![]() 两点处的切线的交点在直线
两点处的切线的交点在直线![]() 上,证明:直线
上,证明:直线![]() 过定点,并求此定点坐标.
过定点,并求此定点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】算盘是中国传统的计算工具,其形长方,周为木框,内贯直柱,俗称“档”,档中横以梁,梁上两珠,每珠作数五,梁下五珠,每珠作数一.算珠梁上部分叫上珠,梁下部分叫下珠.例如:在十位档拨上一颗上珠和一颗下珠,个位档拨上一颗上珠,则表示数字65.若在个、十、百、千位档中随机选择一档拨一颗上珠,再随机选择两个档位各拨一颗下珠,则所拨数字大于200的概率为( ).

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com