
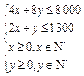 .
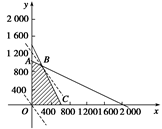
.
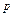 =
=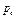 满足
满足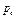 =15x+20y,且点(x,y)属于
=15x+20y,且点(x,y)属于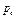 元利润的生产方案.
元利润的生产方案.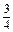 的平行线,且p越大,相应的直线位置越高;p越小,相应的直线位置越低.按题意,要求p的最大值,需把直线p=15x+20y尽量地往上平移,又考虑到x,y的允许范围,
的平行线,且p越大,相应的直线位置越高;p越小,相应的直线位置越低.按题意,要求p的最大值,需把直线p=15x+20y尽量地往上平移,又考虑到x,y的允许范围,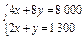 ,得B(200,900),
,得B(200,900),

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源:不详 题型:解答题
 | 甲 | 乙 | 生产能力 (小时/月) |
| 工序(1) | 6 | 12 | 120 |
| 工序(2) | 8 | 4 | 64 |
| 单位利润(千元) | 20 | 24 | |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
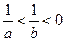 ,则
,则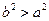 ;
;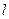 ,平面
,平面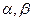 为不重合的两个平面.若
为不重合的两个平面.若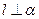 ,且
,且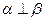 ,则
,则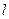 ∥
∥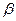 ;
;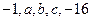 成等比数列,则
成等比数列,则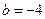 ;
;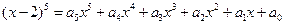 ,则
,则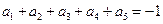 .
. .(写出所有真命题的序号)
.(写出所有真命题的序号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com