
| 篮球 | 排球 | 总计 | |
| 男同学 | 16 | 6 | 22 |
| 女同学 | 8 | 12 | 20 |
| 总计 | 24 | 18 | 42 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (Ⅰ)由表格数据可得K2的观测值,k≈4.582,可得4.582>3.841,根据“独立性检验原理”即可得出结论.
(Ⅱ)①从“排球小组”的18位同学中,要选取3位同学;
②由题知从7人中任意选出2人的方法数为21种,甲、乙两人至少有一人参加校排球队有11种方法,即可求出甲、乙两人至少有一人参加校排球队的概率.
解答 解:(Ⅰ)由表中数据得K2的观测值k=$\frac{42×(16×12-8×6)^{2}}{24×18×20×22}$=$\frac{252}{55}$≈4.582>3.841.…(3分)
所以,据此统计有95%的把握认为参加“篮球小组”或“排球小组”与性别有关.…(6分)
(Ⅱ)①从“排球小组”的18位同学中,要选取3位同学. …(8分)
②由题知从7人中任意选出2人的方法数为21种,甲、乙两人至少有一人参加校排球队有11种方法.
所以甲、乙两人至少有一人参加校排球队的概率是$\frac{11}{21}$ …(12分)
点评 本题考查了独立性检验原理、分层抽样及概率的计算,考查了推理能力与计算能力,属于中档题.


 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:选择题
| A. | 选择结构中不含有顺序结构 | |
| B. | 选择结构、循环结构和顺序结构在流程图中一定是并存的 | |
| C. | 循环结构中一定包含选择结构 | |
| D. | 选择结构中一定有循环结构 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
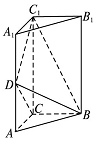 如图,直三棱柱(侧棱垂直于底面)ABC-A1B1C1中,$CA=CB=\frac{1}{2}C{C_1}$,点D棱AA1的中点,且C1D⊥BD.
如图,直三棱柱(侧棱垂直于底面)ABC-A1B1C1中,$CA=CB=\frac{1}{2}C{C_1}$,点D棱AA1的中点,且C1D⊥BD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a∈R | B. | 0≤a≤1 | ||
| C. | $-\frac{1}{2}-\frac{{3\sqrt{3}}}{4}≤a≤-\frac{1}{2}+\frac{{3\sqrt{3}}}{4}$ | D. | a≤0或a≥1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 必要不充分 | ||
| C. | 充分不必要 | D. | 既不充分也不必要 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $±\sqrt{3}$ | B. | $±\sqrt{13}$ | C. | ±4 | D. | $±2\sqrt{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com