
【题目】已知双曲线x2-![]() =1.
=1.
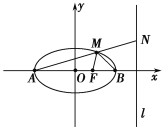
(1)若一椭圆与该双曲线共焦点,且有一交点P(2,3),求椭圆方程.
(2)设(1)中椭圆的左、右顶点分别为A、B,右焦点为F,直线l为椭圆的右准线,N为l上的一动点,且在x轴上方,直线AN与椭圆交于点M.若AM=MN,求∠AMB的余弦值;
(3)设过A、F、N三点的圆与y轴交于P、Q两点,当线段PQ的中点为(0,9)时,求这个圆的方程.
【答案】(1)![]() =1(2)-
=1(2)-![]() (3)x2+y2+2x-18y-8=0
(3)x2+y2+2x-18y-8=0
【解析】(1)∵双曲线焦点为(±2,0),设椭圆方程为![]() =1(a>b>0).
=1(a>b>0).
则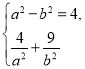 ∴a2=16,b2=12.故椭圆方程为
∴a2=16,b2=12.故椭圆方程为![]() =1.
=1.
(2)由已知,A(-4,0),B(4,0),F(2,0),直线l的方程为x=8.
设N(8,t)(t>0).∵AM=MN,∴M![]() .
.
由点M在椭圆上,得t=6.
故所求的点M的坐标为M(2,3).
所以![]() =(-6,-3),
=(-6,-3),![]() =(2,-3),
=(2,-3),![]() ·
·![]() =-12+9=-3.
=-12+9=-3.
cos∠AMB=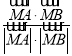 =
=![]() =-
=-![]() .
.
(3)设圆的方程为x2+y2+Dx+Ey+F=0,将A、F、N三点坐标代入,得
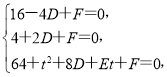 得
得
圆的方程为x2+y2+2x-![]() y-8=0,令x=0,得y2-
y-8=0,令x=0,得y2-![]() y-8=0.
y-8=0.
设P(0,y1),Q(0,y2),则y1,2= .
.
由线段PQ的中点为(0,9),得y1+y2=18,t+![]() =18,
=18,
此时,所求圆的方程为x2+y2+2x-18y-8=0


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
【题目】某人在微信群中发了一个8元“拼手气”红包,被甲、乙、丙三人抢完,若三人均领到整数元,且每人至少领到1元,则甲领到的钱数不少于其他任何人的概率为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,定长为3的线段
中,定长为3的线段![]() 两端点
两端点![]() 、
、![]() 分别在
分别在![]() 轴,
轴,![]() 轴上滑动,
轴上滑动,![]() 在线段
在线段![]() 上,且
上,且![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设点![]() 是轨迹
是轨迹![]() 上一点,从原点
上一点,从原点![]() 向圆
向圆![]() 作两条切线分别与轨迹
作两条切线分别与轨迹![]() 交于点
交于点![]() ,
,![]() ,直线
,直线![]() ,
,![]() 的斜率分别记为
的斜率分别记为![]() ,
,![]() .
.
①求证:![]() ;
;
②求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产甲、乙两种产品所得的利润分别为![]() 和
和![]() (万元),事先根据相关资料得出它们与投入资金
(万元),事先根据相关资料得出它们与投入资金![]() (万元)的数据分别如下表和图所示:其中已知甲的利润模型为
(万元)的数据分别如下表和图所示:其中已知甲的利润模型为![]() ,乙的利润模型为
,乙的利润模型为![]() .(
.(![]() 为参数,且
为参数,且![]() ).
).
|
|
|
|
|
|
|
|
|
|

(1)请根据下表与图中数据,分别求出甲、乙两种产品所得的利润与投入资金![]() (万元)的函数模型
(万元)的函数模型
(2)今将![]() 万资金投入生产甲、乙两种产品,并要求对甲、乙两种产品的投入资金都不低于
万资金投入生产甲、乙两种产品,并要求对甲、乙两种产品的投入资金都不低于![]() 万元.设对乙种产品投入资金
万元.设对乙种产品投入资金![]() (万元),并设总利润为
(万元),并设总利润为![]() (万元),如何分配投入资金,才能使总利润最大?并求出最大总利润.
(万元),如何分配投入资金,才能使总利润最大?并求出最大总利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
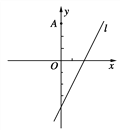
【题目】如下图,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4.设圆C的半径为1,圆心在l上.
(1)若圆心C也在直线y=x-1上,过点A作圆C的切线,求切线的方程;
(2)若圆C上存在点M,使MA=2MO,求圆心C的横坐标a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分)
已知椭圆![]() 的中心在原点,焦点在
的中心在原点,焦点在![]() 轴上,椭圆上的点到焦点的距离的最
轴上,椭圆上的点到焦点的距离的最
小值为![]() ,离心率为
,离心率为![]() 。
。
(I)求椭圆![]() 的方程;
的方程;
(Ⅱ)过点(1,0)作直线![]() 交
交![]() 于
于![]() 、
、![]() 两点,试问:在
两点,试问:在![]() 轴上是否存在一个定点
轴上是否存在一个定点![]() ,使
,使![]() 为定值?若存在,求出这个定点
为定值?若存在,求出这个定点![]() 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为
的定义域为![]() ,若存在区间
,若存在区间![]()
![]() ,使得
,使得![]() 称区间
称区间![]() 为函数
为函数![]() 的“和谐区间”.
的“和谐区间”.
(1)请直接写出函数![]() 的所有的“和谐区间”;
的所有的“和谐区间”;
(2)若![]() 为函数
为函数![]() 的一个“和谐区间”,求
的一个“和谐区间”,求![]() 的值;
的值;
(3)求函数![]() 的所有的“和谐区间”.
的所有的“和谐区间”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,当x≥0时,f(x)=-x2+4x.

(1)求函数f(x)的解析式;
(2)在给定的坐标系中画出函数f(x)在R上的图象(不用列表);
(3)讨论直线y=m(m∈R)与y=f(x)的图象的交点个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com