
【题目】武汉出现的新型冠状病毒是一种可以通过飞沫传播的变异病毒,某药物研究所为筛查该新型冠状病毒,需要检验血液是否为阳性,现有![]() 份血液样本,每份样本取到的可能性均等,有以下两种检验方式:①逐份检验,则需要检验n次;②混合检验,将其中
份血液样本,每份样本取到的可能性均等,有以下两种检验方式:①逐份检验,则需要检验n次;②混合检验,将其中![]() 份血液样本分别取样混合在一起检验.若检验结果为阴性,这k份血液全为阴性,因此这k份血液样本检验一次就够了,如果检验结果为阳性,为了明确这k份血液究竟哪几份为阳性,就要对这k份血液再逐份检验,此时这k份血液的检验次数总共为
份血液样本分别取样混合在一起检验.若检验结果为阴性,这k份血液全为阴性,因此这k份血液样本检验一次就够了,如果检验结果为阳性,为了明确这k份血液究竟哪几份为阳性,就要对这k份血液再逐份检验,此时这k份血液的检验次数总共为![]() 次.假设在接受检验的血液样本中,每份样本的检验结果是阴性还是阳性都是独立的,且每份样本是阳性结果的概率为
次.假设在接受检验的血液样本中,每份样本的检验结果是阴性还是阳性都是独立的,且每份样本是阳性结果的概率为![]() .
.
(1)假设有5份血液样本,其中只有2份为阳性,若采取逐份检验方式,求恰好经过2次检验就能把阳性样本全部检验出来的概率;
(2)现取其中![]() 份血液样本,记采用逐份检验方式,样本需要检验的次数为
份血液样本,记采用逐份检验方式,样本需要检验的次数为![]() ,采用混合检验方式,样本需要检验的总次数为
,采用混合检验方式,样本需要检验的总次数为![]() .
.
(i)试运用概率统计知识,若![]() ,试求P关于k的函数关系式
,试求P关于k的函数关系式![]() ;
;
(ii)若![]() ,采用混合检验方式可以使得这k份血液样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求k的最大值.
,采用混合检验方式可以使得这k份血液样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求k的最大值.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,四边形
中,四边形![]() 为正方形,
为正方形,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 中点.
中点.
[Failed to download image : http://192.168.0.10:8086/QBM/2020/6/18/2487522753945600/2488179565404160/STEM/3bba3a8519b8447aaec6f2ca7eb73ba0.png]
(1)证明:![]() 平面
平面![]() ;
;
(2)已知![]() ,
,![]() ,
,![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为![]() (s为参数),以坐标原点为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(s为参数),以坐标原点为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() ,
,![]() ,直线与曲线C交于A,B两点.
,直线与曲线C交于A,B两点.
(Ⅰ)求直线l的普通方程和曲线C的直角坐标方程;
(Ⅱ)已知点P的极坐标为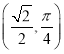 ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C:![]()
![]() 的焦点与抛物线
的焦点与抛物线![]() 的焦点之间的距离为2,且C的离心率为
的焦点之间的距离为2,且C的离心率为![]() ,则下列说法正确的有( ).
,则下列说法正确的有( ).
A.C的渐近线方程为![]() B.C的标准方程为
B.C的标准方程为![]()
C.C的顶点到渐近线的距离为![]() D.曲线
D.曲线![]() 经过C的一个焦点
经过C的一个焦点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表,即杨辉三角,这是数学史上的一个伟大成就.在“杨辉三角”中,第![]() 行的所有数字之和为
行的所有数字之和为![]() ,若去除所有为1的项,依次构成数列
,若去除所有为1的项,依次构成数列![]() ,则此数列的前55项和为( )
,则此数列的前55项和为( )

A. 4072B. 2026C. 4096D. 2048
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以原点为极点,
中,以原点为极点,![]() 轴正半轴为极轴建立极坐标系.已知曲线
轴正半轴为极轴建立极坐标系.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).
为参数).
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,已知点
两点,已知点![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据阅兵领导小组办公室介绍,2019年国庆70周年阅兵有59个方(梯)队和联合军乐团,总规模约1.5万人,是近几次阅兵中规模最大的一次.其中,徒步方队15个.为了保证阅兵式时队列保持整齐,各个方队对受阅队员的身高也有着非常严格的限制,太高或太矮都不行.徒步方队队员,男性身高普遍在175cm至185cm之间;女性身高普遍在163cm至175cm之间,这是常规标准.要求最为严格的三军仪仗队,其队员的身高一般都在184cm至190cm之间.经过随机调查某个阅兵阵营中女子100人,得到她们身高的直方图,如图,记C为事件:“某一阅兵女子身高不低于169cm”,根据直方图得到P(C)的估计值为0.5.

(1)求直方图中a,b的值;
(2)估计这个阵营女子身高的平均值 (同一组中的数据用该组区间的中点值为代表)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com