
【题目】如图,在平面直角坐标系xOy中,已知直线l:x-y-2=0,抛物线C:y2=2px(p>0).
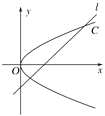
(1)若直线l过抛物线C的焦点,求抛物线C的方程;
(2)当p=1时,若抛物线C上存在关于直线l对称的相异两点P和Q.求线段PQ的中点M的坐标.
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:
【题目】某省高中男生身高统计调查数据显示:全省100000名男生的身高服从正态分布N(170.5,16).现从某学校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5cm之间,将测量结果按如下方式分成6组:第1组[157.5,162.5),第2组[162.5,167.5),…,第6组[182.5,187.5],如图是按上述分组方法得到的频率分布直方图. 
(1)试评估该校高三年级男生的平均身高;
(2)求这50名男生身高在177.5cm以上(含177.5cm)的人数;
(3)在这50名男生身高在177.5cm以上(含177.5cm)的人中任意抽取2人,该2人中身高排名(从高到低)在全省前130名的人数记为ξ,求ξ的分布列和数学期望.
参考数据:若ξ~N(μ,σ2),则P(μ﹣σ<ξ≤μ+σ)=0.6826,P(μ﹣2σ<ξ≤μ+2σ)=0.9544,P(μ﹣3σ<ξ≤μ+3σ)=0.9974.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的奇函数f(x)满足f(x+2)=-f(x),当0≤x≤1时,f(x)=x,
(1)试画出f(x),x∈[-3,5]的图象;
(2)求f(37.5);
(3)常数a∈(0,1),y=a与f(x),x∈[-3,5]的图象相交,求所有交点横坐标之和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,A,B,C三点满足![]() 。
。
(1)求证:A,B,C三点共线;
(2)若A(1,cosx),B(1+sinx,cosx),且x∈[0, ![]() ],函数f(x)=
],函数f(x)=![]() (2m+
(2m+![]() )|
)|![]() |+m2的最小值为5,求实数m的值。
|+m2的最小值为5,求实数m的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】太原五中是一所有着百年历史的名校,图1是某一阶段来我校参观学习的外校人数统计茎叶图,第1次到第14次参观学习人数依次记为A1 , A2 , …,A14 , 图2是统计茎叶图中人数在一定范围内的一个算法流程图,那么算法流程图输出的结果是 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱柱ABCD﹣A1B1C1D1中,底面ABCD是梯形,AD∥BC,侧面ABB1A1为菱形,∠DAB=∠DAA1 . 
(1)求证:A1B⊥AD;
(2)若AD=AB=2BC,∠A1AB=60°,点D在平面ABB1A1上的射影恰为线段A1B的中点,求平面DCC1D1与平面ABB1A1所成锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com