[题目]已知Sn表示数列{an}的前n项和.若对任意的n∈N*满足an+1＝an+a2 . 且a3＝2.则S2016＝( )A.1006×2013B.1006×2014C.1008×2015D.1007×2015 题目和参考答案——青夏教育精英家教网—

【题目】已知Sn表示数列{an}的前n项和，若对任意的n∈N*满足an＋1＝an＋a2 ，且a3＝2，则S2016＝( )
A.1006×2013
B.1006×2014
C.1008×2015
D.1007×2015

【答案】C
【解析】解答：在an+1=an+a2中，令n=1，得a2=a1+a2 ， a1=0，令n=2，得a3=2=2a2 ， a2=1，于是an＋1-an=1，故数列{an}是首项为0，公差为1的等差数列，∴S2016= =1008×2015．故选：C．
分析：
由已知条件推导出数列{an}是首项为0，公差为1的等差数列，由此能求出S2016 ．
【考点精析】本题主要考查了等差数列的前n项和公式的相关知识点，需要掌握前n项和公式：才能正确解答此题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】甲、乙两校各有3名教师报名支教，期中甲校2男1女，乙校1男2女．

（1）若从甲校和乙校报名的教师中各任选1名，写出所有可能的结果，并求选出的2名教师性别相同的概率；

（2）若从报名的6名教师中任选2名，写出所有可能的结果，并求选出的2名教师来自同一学校的概率．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数的反函数为，等比数列{an}的公比为2，若，则 =（）
A.21004×2016
B.21005×2015
C.21005×2016
D.21008×2015

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在圆上任取一点，过点向轴作垂线段，垂足为，当点在圆上运动时，线段的中点的轨迹为.

(1)求曲线的方程；

(2)过点(0，－2)作直线与交于两点，(O为原点)，求三角形面积的最大值，并求此时的直线的方程．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设f（x）＝（1﹣m）lnx++nx（m，n是常数）．

（1）若m＝0，且f（x）在（1，2）上单调递减，求n的取值范围；

（2）若m＞0，且n＝﹣1，求f（x）的单调区间．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知为等差数列，公差（），且（）
（1）求证：当取不同自然数时，此方程有公共根；
（2）若方程不同的根依次为，，， …，， …，求证：数列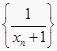为等差数列。

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】一列火车从重庆驶往北京，沿途有n个车站（包括起点站重庆和终点站北京）．车上有一邮政车厢，每停靠一站便要卸下火车已经过的各站发往该站的邮袋各1个，同时又要装上该站发往以后各站的邮袋各1个，设从第k站出发时，邮政车厢内共有邮袋ak个（k=1，2，…，n）．
（1）求数列{ak}的通项公式；
（2）当k为何值时，ak的值最大，求出ak的最大值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】若直线ax﹣by+2=0（a＞0，b＞0）和函数f（x）=ax+1+1（a＞0且a≠1）的图象恒过同一个定点，则当 + 取最小值时，函数f（x）的解析式是．