
【题目】某北方村庄4个草莓基地,采用水培阳光栽培方式种植的草莓个大味美,一上市便成为消费者争相购买的对象.光照是影响草莓生长的关键因素,过去50年的资料显示,该村庄一年当中12个月份的月光照量X(小时)的频率分布直方图如下图所示(注:月光照量指的是当月阳光照射总时长).
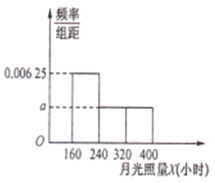
(1)求月光照量![]() (小时)的平均数和中位数;
(小时)的平均数和中位数;
(2)现准备按照月光照量来分层抽样,抽取一年中的4个月份来比较草莓的生长状况,问:应在月光照量![]() ,
,![]() ,
,![]() 的区间内各抽取多少个月份?
的区间内各抽取多少个月份?
(3)假设每年中最热的5,6,7,8,9,10月的月光照量![]() 是大于等于240小时,且6,7,8月的月光照量
是大于等于240小时,且6,7,8月的月光照量![]() 是大于等于320小时,那么,从该村庄2018年的5,6,7,8,9,10这6个月份之中随机抽取2个月份的月光照量进行调查,求抽取到的2个月份的月光照量
是大于等于320小时,那么,从该村庄2018年的5,6,7,8,9,10这6个月份之中随机抽取2个月份的月光照量进行调查,求抽取到的2个月份的月光照量![]() (小时)都不低于320的概率.
(小时)都不低于320的概率.
【答案】(1)平均数为![]() (小时);中位数为240(小时)(2)
(小时);中位数为240(小时)(2)![]() (3)
(3)![]()
【解析】
(1)利用各频率之和为1,计算出![]() ,然后根据频率分布直方图以及平均数,中位数的求法,可得结果.
,然后根据频率分布直方图以及平均数,中位数的求法,可得结果.
(2)根据月光照量![]() 、
、![]() 、
、![]() 的频率之比为
的频率之比为![]() ,结合分层抽样的方法,可得结果.
,结合分层抽样的方法,可得结果.
(3)采用列举法,将“6个月份之中随机抽取2个月份”所有情况列举出来,并计算“抽取到的2个月份的月光照量![]() (小时)都不低于320”的个数,结合古典概型可得结果.
(小时)都不低于320”的个数,结合古典概型可得结果.
(1)根据各频率之和为1,
则![]() ,
,
解得![]() .
.
月光照量![]() (小时)的平均数为
(小时)的平均数为
![]()
所以![]() (小时)
(小时)
设月光照量![]() (小时)的中位数为
(小时)的中位数为![]() ,
,
则![]() .根据中位数的定义,
.根据中位数的定义,
其左右两边的频率相等,都为0.5,可得
![]() ,
,
解得![]() .
.
所以月光照量![]() (小时)的中位数为240(小时).
(小时)的中位数为240(小时).
(2)因为月光照量![]() 、
、![]() 、
、
![]() 的频率之比为
的频率之比为![]() ,
,
所以若准备按照月光照量来分层抽样,
抽取一年中的4个月份来比较草莓的生长状况,
那么,抽取的月光照量![]() ,
,![]() ,
,
![]() 的月份数分别为
的月份数分别为
![]() .
.
(3)由题意,
月光照量![]() 的有5,9,10月,
的有5,9,10月,
月光照量![]() 的有6,7,8月,
的有6,7,8月,
故从该村庄2018年的5,6,7,8,9,10月份
之中随机抽取2个月份的月光照量![]() (小时)
(小时)
进行调查,所有的情况有:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() 共15种;
共15种;
其中,抽取到的2个月份的月光照量
![]() (小时)都不低于320的情况有:
(小时)都不低于320的情况有:
![]() 共3种;
共3种;
故所抽取到的2个月份的月光照量
![]() (小时)都不低于320的概率
(小时)都不低于320的概率![]() .
.


 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:
【题目】2016年“一带一路”沿线64个国家GDP之和约为12.0万亿美元,占全球GDP的![]() ;人口总数约为32.1亿,占全球总人口的
;人口总数约为32.1亿,占全球总人口的![]() ;对外贸易总额(进口额+出口额)约为71885.6亿美元,占全球贸易总额的
;对外贸易总额(进口额+出口额)约为71885.6亿美元,占全球贸易总额的![]() .
.
2016年“一带一路”沿线国家情况
人口(万人) | GDP(亿美元) | 进口额(亿美元) | 出口额(亿美元) | |
蒙古 | 301.4 | 116.5 | 38.7 | 45.0 |
东南亚11国 | 63852.5 | 25802.2 | 11267.2 | 11798.6 |
南亚8国 | 174499.0 | 29146.6 | 4724.1 | 3308.5 |
中亚5国 | 6946.7 | 2254.7 | 422.7 | 590.7 |
西亚、北非19国 | 43504.6 | 36467.5 | 9675.5 | 8850.7 |
东欧20国 | 32161.9 | 26352.1 | 9775.5 | 11388.4 |
关于“一带一路”沿线国家2016年状况,能够从上述资料中推出的是( )
A.超过六成人口集中在南亚地区
B.东南亚和南亚国家GDP之和占全球的![]() 以上
以上
C.平均每个南亚国家对外贸易额超过1000亿美元
D.平均每个东欧国家的进口额高于平均每个西亚、北非国家的进口额
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,
的左、右焦点,![]() 为该椭圆的一条垂直于
为该椭圆的一条垂直于![]() 轴的动弦,直线
轴的动弦,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与直线
与直线![]() 的交点为
的交点为![]() .
.
(1)证明:点![]() 恒在椭圆
恒在椭圆![]() 上.
上.
(2)设直线![]() 与椭圆
与椭圆![]() 只有一个公共点
只有一个公共点![]() ,直线
,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,在平面内是否存在定点
,在平面内是否存在定点![]() ,使得
,使得![]() 恒成立?若存在,求出该点坐标;若不存在,说明理由.
恒成立?若存在,求出该点坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在水平地面上的不同两点处栽有两根笔直的电线杆,假设它们都垂直于地面,则在水平地面上视它们上端仰角相等的点![]() 的轨迹可能是( )
的轨迹可能是( )
①直线 ②圆 ③椭圆 ④抛物线
A.①②B.①③C.①②③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某项娱乐活动的海选过程中评分人员需对同批次的选手进行考核并评分,并将其得分作为该选手的成绩,成绩大于等于![]() 分的选手定为合格选手,直接参加第二轮比赛,大于等于
分的选手定为合格选手,直接参加第二轮比赛,大于等于![]() 分的选手将直接参加竞赛选拔赛.已知成绩合格的
分的选手将直接参加竞赛选拔赛.已知成绩合格的![]() 名参赛选手成绩的频率分布直方图如图所示,其中
名参赛选手成绩的频率分布直方图如图所示,其中![]() 的频率构成等比数列.
的频率构成等比数列.
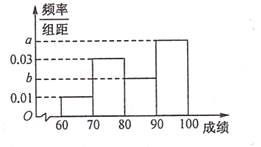
(1)求![]() 的值;
的值;
(2)估计这![]() 名参赛选手的平均成绩;
名参赛选手的平均成绩;
(3)根据已有的经验,参加竞赛选拔赛的选手能够进入正式竞赛比赛的概率为![]() ,假设每名选手能否通过竞赛选拔赛相互独立,现有
,假设每名选手能否通过竞赛选拔赛相互独立,现有![]() 名选手进入竞赛选拔赛,记这
名选手进入竞赛选拔赛,记这![]() 名选手在竞赛选拔赛中通过的人数为随机变量
名选手在竞赛选拔赛中通过的人数为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线C:![]() (
(![]() )的焦点F到直线
)的焦点F到直线![]() 的距离为
的距离为![]() .AB是过抛物线C焦点F的动弦,O是坐标原点,过A,B两点分别作此抛物线的切线,两切线相交于点P.
.AB是过抛物线C焦点F的动弦,O是坐标原点,过A,B两点分别作此抛物线的切线,两切线相交于点P.
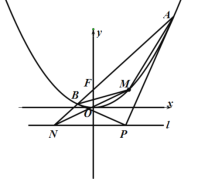
(1)求证:![]() .
.
(2)若动弦AB不经过点![]() ,直线AB与准线l相交于点N,记MA,MB,MN的斜率分别为
,直线AB与准线l相交于点N,记MA,MB,MN的斜率分别为![]() ,
,![]() ,
,![]() .问:是否存在常数λ,使得
.问:是否存在常数λ,使得![]() 在弦AB运动时恒成立?若存在,求λ的值;若不存在,说明理由.
在弦AB运动时恒成立?若存在,求λ的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com