
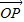 =
=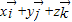 (其中
(其中 分别为x轴、y轴、z轴正方向上的单位向量).有下列命题:
分别为x轴、y轴、z轴正方向上的单位向量).有下列命题: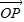 =
=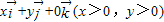 且|
且|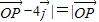
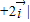 ,则
,则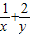 的最小值为2
的最小值为2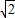

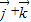 ,若向量
,若向量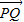 与
与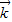 共线且|
共线且|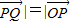 |,则动点P的轨迹是抛物线;
|,则动点P的轨迹是抛物线;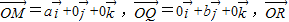 =
=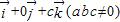 ,则平面MQR内的任意一点A(x,y,z)的坐标必须满足关系式
,则平面MQR内的任意一点A(x,y,z)的坐标必须满足关系式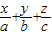 =1;
=1;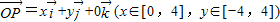 ,
,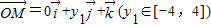 ,
,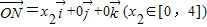 ,若向量
,若向量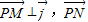 与
与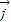 共线且|
共线且|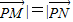 |,则动点P的轨迹是双曲线的一部分.
|,则动点P的轨迹是双曲线的一部分.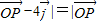
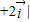 得到两个正数x,y的关系
得到两个正数x,y的关系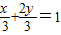 ,求
,求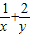 的最小值时只要把“1”代入展开后利用基本不等式求最值;
的最小值时只要把“1”代入展开后利用基本不等式求最值;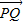 ,由
,由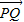 与
与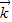 共线且|
共线且|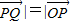 |列式得到动点P的轨迹;
|列式得到动点P的轨迹;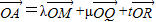 ,且λ+μ+t=1,由坐标相等得到
,且λ+μ+t=1,由坐标相等得到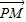 与
与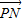 的坐标,利用条件
的坐标,利用条件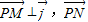 与
与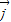 共线且|
共线且|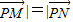 |,列式得到结论.
|,列式得到结论.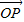 =
=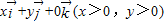 且|
且|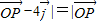
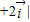 ,
,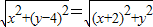 ,即
,即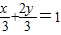 .
. =
=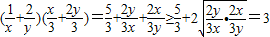 .
.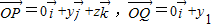
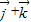 ,
,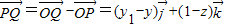 .
.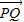 与
与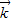 共线且|
共线且|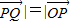 |,得
|,得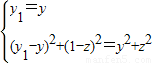 ,
,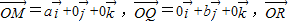 =
=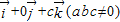 ,则平面MQR内的任意一点
,则平面MQR内的任意一点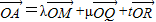 ,即(x,y,z)=λ(a,0,0)+μ(0,b,0)+t(0,0,c)
,即(x,y,z)=λ(a,0,0)+μ(0,b,0)+t(0,0,c)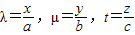 .
.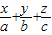 =1.所以③正确;
=1.所以③正确;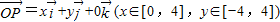 ,
,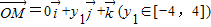 ,
,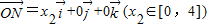 ,得
,得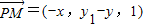 ,
,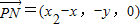 .
.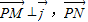 与
与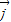 共线且|
共线且|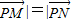 |,得
|,得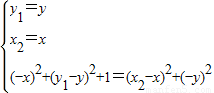 ,整理得:y2-x2=1(0≤x≤4,-4≤y≤4).
,整理得:y2-x2=1(0≤x≤4,-4≤y≤4).

科目:高中数学 来源: 题型:
| A、2 | B、3 | C、6 | D、10 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| OA |
| OB |
| OP |
| QA |
| QB |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com