
【题目】已知焦点在![]() 轴上的椭圆的一个顶点为
轴上的椭圆的一个顶点为![]() ,以右焦点为圆心以3为半径的圆与直线
,以右焦点为圆心以3为半径的圆与直线![]() 相切.
相切.
(1)求椭圆的方程;
(2)设椭圆与直线![]() 相交于不同的两点
相交于不同的两点![]() 、
、![]() .当
.当![]() 时,求三角形
时,求三角形![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)利用焦点到直线的距离等于半径和上顶点坐标可构造方程求得![]() ,进而得到椭圆方程;
,进而得到椭圆方程;
(2)设![]() 为
为![]() 中点,由
中点,由![]() 可知
可知![]() ,将直线方程与椭圆方程联立可得韦达定理的形式,利用韦达定理表示出
,将直线方程与椭圆方程联立可得韦达定理的形式,利用韦达定理表示出![]() ,根据判别式
,根据判别式![]() 可构造不等式求得
可构造不等式求得![]() 的范围;利用弦长公式和点到直线距离公式求得弦长
的范围;利用弦长公式和点到直线距离公式求得弦长![]() 和三角形的高,代入面积公式可整理得到关于
和三角形的高,代入面积公式可整理得到关于![]() 的函数,利用二次函数性质可确定取最大值时
的函数,利用二次函数性质可确定取最大值时![]() 的取值,进而得到最大值.
的取值,进而得到最大值.
(1)设椭圆方程为:![]() .
.
![]() 椭圆焦点在
椭圆焦点在![]() 轴上,且一个顶点为
轴上,且一个顶点为![]() ,则
,则![]() 且
且![]() ,
,
则右焦点![]() ,
,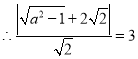 ,解得:
,解得:![]() ,
,
![]() 椭圆方程为:
椭圆方程为:![]() .
.
(2)设![]() ,
,![]() ,
,![]() 为
为![]() 中点,
中点,
由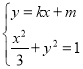 得:
得:![]() ,
,
![]() ,解得:
,解得:![]() …①
…①
则![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,即
,即![]() ,
,
![]() ,代入①中得:
,代入①中得:![]() ,解得:
,解得:![]() ,
,
由![]() 得:
得:![]() ,
,![]() 的取值范围为
的取值范围为![]() .
.
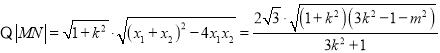 ,
,
原点到直线![]() 的距离
的距离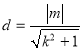 ,
,
![]() ,
,
![]() ,
,![]() 当
当![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.


科目:高中数学 来源: 题型:
【题目】国家规定每年的![]() 月
月![]() 日以后的
日以后的![]() 天为当年的暑假.某钢琴培训机构对
天为当年的暑假.某钢琴培训机构对![]() 位钢琴老师暑假一天的授课量进行了统计,如下表所示:
位钢琴老师暑假一天的授课量进行了统计,如下表所示:
授课量(单位:小时) |
|
|
|
|
|
频数 |
|
|
|
|
|
培训机构专业人员统计近![]() 年该校每年暑假
年该校每年暑假![]() 天的课时量情况如下表:
天的课时量情况如下表:
课时量(单位:天) |
|
|
|
|
|
频数 |
|
|
|
|
|
(同组数据以这组数据的中间值作代表)
(1)估计![]() 位钢琴老师一日的授课量的平均数;
位钢琴老师一日的授课量的平均数;
(2)若以(1)中确定的平均数作为上述一天的授课量.已知当地授课价为![]() 元/小时,每天的各类生活成本为
元/小时,每天的各类生活成本为![]() 元/天;若不授课,不计成本,请依据往年的统计数据,估计一位钢琴老师
元/天;若不授课,不计成本,请依据往年的统计数据,估计一位钢琴老师![]() 天暑假授课利润不少于
天暑假授课利润不少于![]() 万元的概率.
万元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系x0y中,把曲线![]()
![]() α为参数)上每个点的横坐标变为原来的
α为参数)上每个点的横坐标变为原来的![]() 倍,纵坐标不变,得到曲线
倍,纵坐标不变,得到曲线![]() 以坐标原点为极点,以x轴正半轴为极轴,建立极坐标系,曲线
以坐标原点为极点,以x轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程
的极坐标方程![]()
(1)写出![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)设点M在![]() 上,点N在
上,点N在![]() 上,求|MN|的最小值以及此时M的直角坐标.
上,求|MN|的最小值以及此时M的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重.大气污染可引起心悸.呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机的对入院![]() 人进行了问卷调查得到了如下的列联表:
人进行了问卷调查得到了如下的列联表:
患心肺疾病 | 不患心肺疾病 | 合计 | |
男 |
| ||
女 |
| ||
合计 |
|
已知在全部![]() 人中随机抽取
人中随机抽取![]() 人,抽到患心肺疾病的人的概率为
人,抽到患心肺疾病的人的概率为![]() .
.
(1)请将上面的列联表补充完整,并判断是否有![]() 的把握认为患心肺疾病与性别有关?请说明你的理由;
的把握认为患心肺疾病与性别有关?请说明你的理由;
(2)已知在不患心肺疾病的![]() 位男性中,有
位男性中,有![]() 位从事的是户外作业的工作.为了指导市民尽可能地减少因雾霾天气对身体的伤害,现从不患心肺疾病的
位从事的是户外作业的工作.为了指导市民尽可能地减少因雾霾天气对身体的伤害,现从不患心肺疾病的![]() 位男性中,选出
位男性中,选出![]() 人进行问卷调查,求所选的
人进行问卷调查,求所选的![]() 人中至少有一位从事的是户外作业的概率.
人中至少有一位从事的是户外作业的概率.
下面的临界值表供参考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(参考公式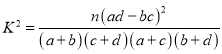 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x|x﹣a|,a∈R.
(1)当f(2)+f(﹣2)>4时,求a的取值范围;
(2)若a>0,x,y∈(﹣∞,a],不等式f(x)≤|y+3|+|y﹣a|恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,以坐标原点
为参数,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,取相同长度单位建立极坐标系,曲线
轴的正半轴为极轴,取相同长度单位建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)设射线![]() 与曲线
与曲线![]() 交于不同于极点的点
交于不同于极点的点![]() ,与曲线
,与曲线![]() 交于不同于极点的点
交于不同于极点的点![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 的图像上存在两个不同的点关于
的图像上存在两个不同的点关于![]() 轴对称,则称函数
轴对称,则称函数![]() 图像上存在一对“偶点”.
图像上存在一对“偶点”.
(1)写出函数![]() 图像上一对“偶点”的坐标;(不需写出过程)
图像上一对“偶点”的坐标;(不需写出过程)
(2)证明:函数![]() 图像上有且只有一对“偶点”;
图像上有且只有一对“偶点”;
(3)若函数![]() 图像上有且只有一对“偶点”,求
图像上有且只有一对“偶点”,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年12月以来,湖北武汉市发现多起病毒性肺炎病例,并迅速在全国范围内开始传播,专家组认为,本次病毒性肺炎病例的病原体初步判定为新型冠状病毒,该病毒存在人与人之间的传染,可以通过与患者的密切接触进行传染.我们把与患者有过密切接触的人群称为密切接触者,每位密切接触者被感染后即被称为患者.已知每位密切接触者在接触一个患者后被感染的概率为![]() ,某位患者在隔离之前,每天有
,某位患者在隔离之前,每天有![]() 位密切接触者,其中被感染的人数为
位密切接触者,其中被感染的人数为![]() ,假设每位密切接触者不再接触其他患者.
,假设每位密切接触者不再接触其他患者.
(1)求一天内被感染人数为![]() 的概率
的概率![]() 与
与![]() 、
、![]() 的关系式和
的关系式和![]() 的数学期望;
的数学期望;
(2)该病毒在进入人体后有14天的潜伏期,在这14天的潜伏期内患者无任何症状,为病毒传播的最佳时间,设每位患者在被感染后的第二天又有![]() 位密切接触者,从某一名患者被感染,按第1天算起,第
位密切接触者,从某一名患者被感染,按第1天算起,第![]() 天新增患者的数学期望记为
天新增患者的数学期望记为![]() .
.
(i)求数列![]() 的通项公式,并证明数列
的通项公式,并证明数列![]() 为等比数列;
为等比数列;
(ii)若戴口罩能降低每位密切接触者患病概率,降低后的患病概率![]() ,当
,当![]() 取最大值时,计算此时
取最大值时,计算此时![]() 所对应的
所对应的![]() 值和此时
值和此时![]() 对应的
对应的![]() 值,根据计算结果说明戴口罩的必要性.(取
值,根据计算结果说明戴口罩的必要性.(取![]() )
)
(结果保留整数,参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图统计了截止到2019年年底中国电动汽车充电桩细分产品占比及保有量情况,关于这5次统计,下列说法正确的是( )
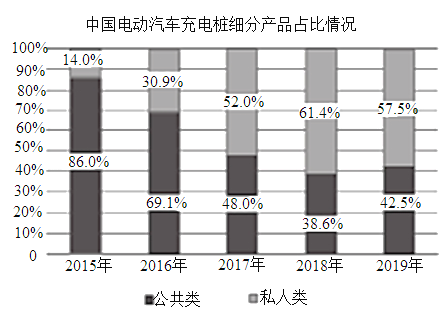
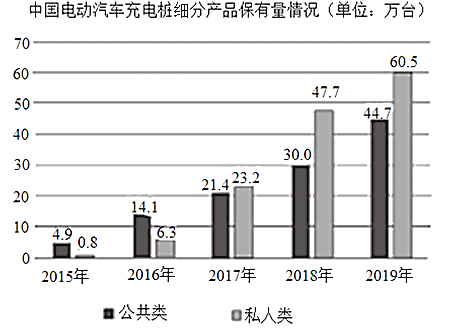
A.私人类电动汽车充电桩保有量增长率最高的年份是2018年
B.公共类电动汽车充电桩保有量的中位数是25.7万台
C.公共类电动汽车充电桩保有量的平均数为23.12万台
D.从2017年开始,我国私人类电动汽车充电桩占比均超过50%
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com