
【题目】在平面直角坐标系xOy中,已知曲线C的参数方程为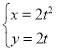 (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为ρ(
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为ρ(![]() cosθ+sinθ)=8.
cosθ+sinθ)=8.
(1)求曲线C和直线l的直角坐标方程;
(2)若射线m的极坐标方程为θ![]() (ρ≥0),设m与C相交于点M(非坐标原点),m与l相交于点N,点P(6,0),求△PMN的面积.
(ρ≥0),设m与C相交于点M(非坐标原点),m与l相交于点N,点P(6,0),求△PMN的面积.
科目:高中数学 来源: 题型:
【题目】十九大报告要求,确保到2020年我国现行标准下农村贫困人口实现脱贫,贫困县全部摘帽,解决区域性整体贫困,做到脱真贫、真脱贫.某贫困地区扶贫办积极贯彻落实国家精准扶贫的政策要求,带领农村地区人民群众脱贫奔小康,扶贫办计划为某农村地区购买农机机器,假设该种机器使用三年后即被淘汰.农机机器制造商对购买该机器的客户推出了两种销售方案:
方案一:每台机器售价7000元,三年内可免费保养2次,超过2次每次收取保养费200元;
方案二:每台机器售价7050元,三年内可免费保养3次,超过3次每次收取保养费100元.
扶贫办需要决策在购买机器时应该选取那种方案,为此搜集并整理了50台这种机器在三年使用期内保养的次数,得下表:
保养次数 | 0 | 1 | 2 | 3 | 4 | 5 |
台数 | 1 | 10 | 19 | 14 | 4 | 2 |
记x表示1台机器在三年使用期内的保养次数.
(1)用样本估计总体的思想,求“x不超过3”的概率;
(2)按照两种销售方案,分别计算这50台机器三年使用期内的总费用(总费用=售价+保养费),以每台每年的平均费用作为决策依据,扶贫办选择那种销售方案购买机器更合算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线l过抛物线C:y2=4x的焦点F且与C交于A(x1,y1),B(x2,y2)两点,则y1y2=_____.过A,B两点分别作抛物线C的准线的垂线,垂足分别为P,Q,准线与x轴的交点为M,四边形FAPM的面积记为S1,四边形FBQM的面积记为S2,则S1S2﹣3|AF||BF|=_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,且asinB![]() bcosA+a=bcosC+ccosB.
bcosA+a=bcosC+ccosB.
(1)求A;
(2)若a![]() ,点D在BC上,且AD⊥AC,当△ABC的周长取得最大值时,求BD的长.
,点D在BC上,且AD⊥AC,当△ABC的周长取得最大值时,求BD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是抛物线
是抛物线![]() 的焦点,过点
的焦点,过点![]() 且与坐标轴不垂直的直线交抛物线于
且与坐标轴不垂直的直线交抛物线于![]() 、
、![]() 两点,交抛物线的准线于点
两点,交抛物线的准线于点![]() ,其中
,其中![]() ,
,![]() .过点
.过点![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,直线
,直线![]() 交抛物线于点
交抛物线于点![]() .
.
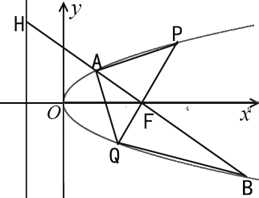
(1)求![]() 的值;
的值;
(2)求四边形![]() 的面积
的面积![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年1月3日嫦娥四号探测器成功实现人类历史上首次月球背面软着陆,我国航天事业取得又一重大成就,实现月球背面软着陆需要解决的一个关键技术问题是地面与探测器的通讯联系.为解决这个问题,发射了嫦娥四号中继星“鹊桥”,鹊桥沿着围绕地月拉格朗日![]() 点的轨道运行.
点的轨道运行.![]() 点是平衡点,位于地月连线的延长线上.设地球质量为M1,月球质量为M2,地月距离为R,
点是平衡点,位于地月连线的延长线上.设地球质量为M1,月球质量为M2,地月距离为R,![]() 点到月球的距离为r,根据牛顿运动定律和万有引力定律,r满足方程:
点到月球的距离为r,根据牛顿运动定律和万有引力定律,r满足方程:
![]() .
.
设![]() ,由于
,由于![]() 的值很小,因此在近似计算中
的值很小,因此在近似计算中![]() ,则r的近似值为
,则r的近似值为
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com