
【题目】已知函数![]() .
.
(1)解关于![]() 的不等式
的不等式![]() ;
;
(2)若对于任意![]() ,
,![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析(2)![]()
【解析】
(1)通过讨论![]() 的范围,求出不等式的解集即可;
的范围,求出不等式的解集即可;
(2)将不等式恒成立转化为![]() ,
,![]() ,求出函数的最小值即可.
,求出函数的最小值即可.
(1)由不等式![]() ,
,
当![]() 时,则
时,则![]() ,此时不等式的解集为
,此时不等式的解集为![]() ,
,
当![]() 时,则
时,则![]() ,此时不等式的解集为
,此时不等式的解集为![]() ,
,
当![]() 时,则
时,则![]() ,此时不等式的解集为
,此时不等式的解集为![]() ,
,
当![]() 时,则
时,则![]() ,此时不等式的解集为
,此时不等式的解集为![]() ,
,
当![]() 时,则
时,则![]() ,此时不等式的解集为
,此时不等式的解集为![]() ,
,
当![]() 时,则
时,则![]() ,此时不等式的解集为
,此时不等式的解集为![]() ,
,
综上,当![]() 时,不等式的解集为
时,不等式的解集为![]() ;当
;当![]() 时,不等式的解集为
时,不等式的解集为![]() ;当
;当![]() 时,不等式的解集为
时,不等式的解集为![]() ;当
;当![]() 时,不等式的解集为
时,不等式的解集为![]() ;当
;当![]() 时,不等式的解集为
时,不等式的解集为![]() ;当
;当![]() 时,不等式的解集为
时,不等式的解集为![]() .
.
(2)由题意,对任意![]() ,
,![]() 恒成立,
恒成立,
即![]() 对任意
对任意![]() 恒成立,
恒成立,
分离参数得![]() 对任意
对任意![]() 恒成立,
恒成立,
所以![]() ,
,![]() ,
,
因![]() ,当且仅当
,当且仅当![]() ,即
,即![]() 时取等号,
时取等号,
所以![]() ,又
,又![]() ,
,
故实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知i为虚数单位,a为实数,复数z=(1﹣2i)(a+i)在复平面内对应的点为M,则![]() “”是“点M在第四象限”的( )
“”是“点M在第四象限”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,设点集![]() ,
,![]() 令
令![]() .从集合Mn中任取两个不同的点,用随机变量X表示它们之间的距离.
.从集合Mn中任取两个不同的点,用随机变量X表示它们之间的距离.
(1)当n=1时,求X的概率分布;
(2)对给定的正整数n(n≥3),求概率P(X≤n)(用n表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生参加4门学科的学业水平测试,每门得![]() 等级的概率都是
等级的概率都是![]() ,该学生各学科等级成绩彼此独立.规定:有一门学科获
,该学生各学科等级成绩彼此独立.规定:有一门学科获![]() 等级加1分,有两门学科获
等级加1分,有两门学科获![]() 等级加2分,有三门学科获
等级加2分,有三门学科获![]() 等级加3分,四门学科全获
等级加3分,四门学科全获![]() 等级则加5分,记
等级则加5分,记![]() 表示该生的加分数,
表示该生的加分数, ![]() 表示该生获
表示该生获![]() 等级的学科门数与未获
等级的学科门数与未获![]() 等级学科门数的差的绝对值.
等级学科门数的差的绝对值.
(1)求![]() 的数学期望;
的数学期望;
(2)求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点![]() ,
,![]() ,动点
,动点![]() 满足直线
满足直线![]() 与
与![]() 的斜率之积为
的斜率之积为![]() .记点
.记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求![]() 的方程,并说明
的方程,并说明![]() 是什么曲线;
是什么曲线;
(2)若![]() ,
,![]() 是曲线
是曲线![]() 上的动点,且直线
上的动点,且直线![]() 过点
过点![]() ,问在
,问在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() ?若存在,请求出定点
?若存在,请求出定点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三名工人加工同一种零件,他们在一天中的工作情况如图所示,其中点![]() 的横、纵坐标分别为第
的横、纵坐标分别为第![]() 名工人上午的工作时间和加工的零件数,点
名工人上午的工作时间和加工的零件数,点![]() 的横、纵坐标分别为第
的横、纵坐标分别为第![]() 名工人下午的工作时间和加工的零件数,
名工人下午的工作时间和加工的零件数,![]() .记
.记![]() 为第
为第![]() 名工人在这一天中加工的零件总数,记
名工人在这一天中加工的零件总数,记![]() 为第
为第![]() 名工人在这一天中平均加工的零件数,则
名工人在这一天中平均加工的零件数,则![]() ,
,![]() ,
,![]() 中的最大值与
中的最大值与![]() ,
,![]() ,
,![]() 中的最大值分别是( )
中的最大值分别是( )

A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校要在一条水泥路边安装路灯,其中灯杆的设计如图所示,AB为地面,CD,CE为路灯灯杆,CD⊥AB,∠DCE=![]() ,在E处安装路灯,且路灯的照明张角∠MEN=
,在E处安装路灯,且路灯的照明张角∠MEN=![]() .已知CD=4m,CE=2m.
.已知CD=4m,CE=2m.
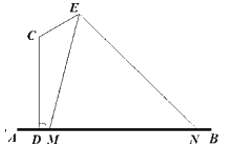
(1)当M,D重合时,求路灯在路面的照明宽度MN;
(2)求此路灯在路面上的照明宽度MN的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com