
【题目】第23届冬季奥运会于2018年2月9日至2月25日在韩国平昌举行,期间正值我市学校放寒假,寒假结束后,某校工会对全校教职工在冬季奥运会期间每天收看比赛转播的时间作了一次调查,得到如下频数分布表:

(1)若讲每天收看比赛转播时间不低于3小时的教职工定义为“体育达人”,否则定义为“非体育达人”,请根据频数分布表补全![]() 列联表:
列联表:

并判断能否有90%的把握认为该校教职工是否为“体育达人”与“性别”有关;
(2)在全校“体育达人”中按性别分层抽样抽取6名,再从这6名“体育达人”中选取2名作冬奥会知识讲座.记其中女职工的人数为![]() ,求的
,求的![]() 分布列与数学期望.
分布列与数学期望.
附表及公式:
![]()
![]() .
.
科目:高中数学 来源: 题型:
【题目】【题目】已知抛物线C:y2=2x,过点(2,0)的直线l交C于A,B两点,圆M是以线段AB为直径的圆.
(1)证明:坐标原点O在圆M上;
(2)设圆M过点P(4,-2),求直线l与圆M的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)当![]() 时,求满足方程
时,求满足方程![]() 的
的![]() 的值;
的值;
(2)若函数![]() 是定义在R上的奇函数.
是定义在R上的奇函数.
①若存在![]() ,使得不等式
,使得不等式![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
②已知函数![]() 满足
满足![]() ,若对任意
,若对任意![]() 且
且![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的最大值
的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的三个顶点
的三个顶点![]() ,
,![]() ,
,![]() ,其外接圆为
,其外接圆为![]() .对于线段
.对于线段![]() 上的任意一点
上的任意一点![]() ,
,
若在以![]() 为圆心的圆上都存在不同的两点
为圆心的圆上都存在不同的两点![]() ,使得点
,使得点![]() 是线段
是线段![]() 的中点,则
的中点,则![]() 的半径
的半径![]() 的取值范围__________.
的取值范围__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,E,F,G分别是AB,CC1,AD的中点.
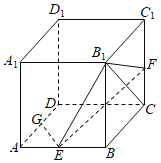
(1)求异面直线EG与B1C所成角的大小;
(2)棱CD上是否存在点T,使AT∥平面B1EF?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】基于移动互联技术的共享单车被称为“新四大发明”之一,短时间内就风靡全国,带给人们新的出行体验.某共享单车运营公司的市场研究人员为了解公司的经营状况,对该公司最近六个月内的市场占有率进行了统计,结果如下表:
月份 | 2017.8 | 2017.9 | 2017.10 | 2017.11 | 2017.12 | 2018.1 |
月份代码x | 1 | 2 | 3 | 4 | 5 | 6 |
市 场占有率y(%) | 11 | 13 | 16 | 15 | 20 | 21 |
(1)请在给出的坐标纸中作出散点图;
(2)求y关于x的线性回归方程,并预测该公司2018年2月份的市场占有率;
参考公式:回归直线方程为![]() 其中:
其中: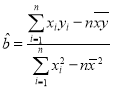 ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com