5

分析:根据a>0,b>0,且a+b=1,可得(a+1)+(b+1)=3,(a+1>1,b+1>1),可令

=

cosθ,

=

sinθ,利用三角函数中的辅助角公式即可解决问题.
解答:∵a>0,b>0,且a+b=1,∴(a+1)+(b+1)=3,(a+1>1,b+1>1),
令

=

cosθ,

=

sinθ,
则
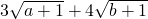
=3

cosθ+4

sinθ=

(3cosθ+4sinθ)=5

sin(θ+φ)(其中tanφ=

).
故答案为:

.
点评:本题考查基本不等式,难点在于由“a+b=1,可得(a+1)+(b+1)=3,即
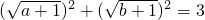
”从而进行三角换元,考查学生的转化思想,属于难题.

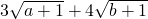 的最大值是________.
的最大值是________.