
【题目】已知函数 ![]() ,a为正常数.
,a为正常数.
(1)若f(x)=lnx+φ(x),且 ![]() ,求函数f(x)的单调增区间;
,求函数f(x)的单调增区间;
(2)若g(x)=|lnx|+φ(x),且对任意x1 , x2∈(0,2],x1≠x2 , 都有 ![]() ,求a的取值范围.
,求a的取值范围.
【答案】
(1)解: 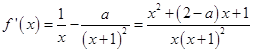 ,
,
∵ ![]() ,令f′(x)>0,得x>2,或
,令f′(x)>0,得x>2,或 ![]() ,
,
∴函数f(x)的单调增区间为 ![]() ,(2,+∞)
,(2,+∞)
(2)解:∵ ![]() ,
,
∴ ![]() ,
,
∴ 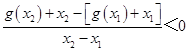 ,
,
设h(x)=g(x)+x,依题意,h(x)在(0,2]上是减函数.
当1≤x≤2时, ![]() ,
, ![]() ,
,
令h′(x)≤0,得: ![]() 对x∈[1,2]恒成立,
对x∈[1,2]恒成立,
设 ![]() ,则
,则 ![]() ,
,
∵1≤x≤2,∴ ![]() ,
,
∴m(x)在[1,2]上递增,则当x=2时,m(x)有最大值为 ![]() ,
,
∴ ![]()
当0<x<1时, ![]() ,
, ![]() ,
,
令h′(x)≤0,得: ![]() ,
,
设 ![]() ,则
,则 ![]() ,
,
∴t(x)在(0,1)上是增函数,
∴t(x)<t(1)=0,
∴a≥0.
综上所述, ![]()
【解析】(1)先对函数y=f(x)进行求导,然后令导函数大于0(或小于0)求出x的范围,根据f′(x)>0求得的区间是单调增区间,f′(x)<0求得的区间是单调减区间,即可得到答案.(2)设h(x)=g(x)+x,依题意得出h(x)在(0,2]上是减函数.下面对x分类讨论:①当1≤x≤2时,②当0<x<1时,利用导数研究函数的单调性从及最值,即可求得求a的取值范围.
【考点精析】关于本题考查的导数的几何意义和利用导数研究函数的单调性,需要了解通过图像,我们可以看出当点![]() 趋近于
趋近于![]() 时,直线
时,直线![]() 与曲线相切.容易知道,割线
与曲线相切.容易知道,割线![]() 的斜率是
的斜率是![]() ,当点
,当点![]() 趋近于
趋近于![]() 时,函数
时,函数![]() 在
在![]() 处的导数就是切线PT的斜率k,即
处的导数就是切线PT的斜率k,即![]() ;一般的,函数的单调性与其导数的正负有如下关系: 在某个区间
;一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能得出正确答案.
在这个区间单调递减才能得出正确答案.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:
【题目】已知c>0,且c≠1,设p:函数y=cx在R上单调递减;q:函数f(x)=x2﹣2cx+1在( ![]() ,+∞)上为增函数,若“p且q”为假,“p或q”为真,求实数c的取值范围.
,+∞)上为增函数,若“p且q”为假,“p或q”为真,求实数c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是R上的奇函数,且当x>0时,f(x)=-2x2+4x+3.
(1)求f(x)的表达式;
(2)画出f(x)的图象,并指出f(x)的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=e2x+1﹣2mx﹣ ![]() m,其中m∈R,e为自然对数底数.
m,其中m∈R,e为自然对数底数.
(1)讨论函数f(x)的单调性;
(2)若不等式f(x)≥n对任意x∈R都成立,求mn的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有2名男生和3名女生. (Ⅰ)若其中2名男生必须相邻排在一起,则这5人站成一排,共有多少种不同的排法?
(Ⅱ)若男生甲既不能站排头,也不能站排尾,这5人站成一排,共有多少种不同的排法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】里约热内卢奥运会正在如火如荼的进行,奥运会纪念品销售火爆,已知某种纪念品的单价是5元,买x(x∈{1,2,3,4,5})件该纪念品需要y元.试用函数的三种表示法表示函数y=f(x).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,a为正常数.
,a为正常数.
(1)若f(x)=lnx+φ(x),且 ![]() ,求函数f(x)的单调增区间;
,求函数f(x)的单调增区间;
(2)若g(x)=|lnx|+φ(x),且对任意x1 , x2∈(0,2],x1≠x2 , 都有 ![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,且
,且 ![]() .
.
(1)试求 ![]() 的值;
的值;
(2)用定义证明函数 ![]() 在
在 ![]() 上单调递增;
上单调递增;
(3)设关于 ![]() 的方程
的方程 ![]() 的两根为
的两根为 ![]() ,试问是否存在实数
,试问是否存在实数 ![]() ,使得不等式
,使得不等式 ![]() 对任意的
对任意的 ![]() 及
及 ![]() 恒成立?若存在,求出
恒成立?若存在,求出 ![]() 的取值范围;若不存在说明理由.
的取值范围;若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司有A、B两个景点,位于一条小路(直道)的同侧,分别距小路![]() km和2
km和2![]() km,且A、B景点间相距2 km,今欲在该小路上设一观景点,使两景点在同时进入视线时有最佳观赏和拍摄效果,则观景点应设于____.
km,且A、B景点间相距2 km,今欲在该小路上设一观景点,使两景点在同时进入视线时有最佳观赏和拍摄效果,则观景点应设于____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com