
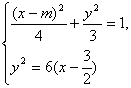 (其中θ为参数)和抛物线
(其中θ为参数)和抛物线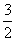 (其中t为参数).
(其中t为参数).(1)是否存在这样的m值,使得该椭圆与该抛物线有四个不同的交点?请说明理由.
(2)当m取何值时,该椭圆与该抛物线的交点与坐标原点的距离等于这个交点与该椭圆中心的距离?
思路分析:本题所给的两条曲线都是其参数方程的形式,如果该题直接根据其参数方程来进行计算也许比较麻烦,所以本题可考虑将参数消去,转化为普通方程来求解,从而达到目的.与此同时,本题也是对于学生的函数方面的知识的一个考查.
解:(1)将题中的椭圆及抛物线方程分别消参化为普通方程,并联立得方程组
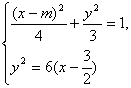 消去y得x2+(8-2m)x+m2-16=0,令f(x)=x2+(8-2m)x+m2-16.
消去y得x2+(8-2m)x+m2-16=0,令f(x)=x2+(8-2m)x+m2-16.
由抛物线方程知x≥![]() ,则椭圆与抛物线有四个交点的充要条件是方程f(x)=0在[
,则椭圆与抛物线有四个交点的充要条件是方程f(x)=0在[![]() ,+∞)上有两个不等的实根,即
,+∞)上有两个不等的实根,即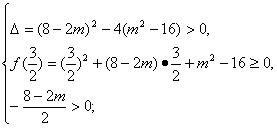
即
显然此不等式组无解,故满足题设条件的m值不存在.
(2)由Δ≥0得m≤4,又知椭圆的半长轴a=2,抛物线的顶点为(![]() ,0),故当-2≤m-
,0),故当-2≤m-![]() ≤2,-
≤2,-![]() ≤m≤
≤m≤![]() 时,椭圆与抛物线必相交.
时,椭圆与抛物线必相交.
若满足题设条件,可有以下两种情况:①椭圆中心与原点重合,此时m=0;②椭圆与抛物线的交点在椭圆中心与原点所连线段的垂直平分线上,即交点在直线x=![]() 上,将x=
上,将x=![]() 代入x2+(8-2m)x+m2-16=0,得m2+16m-64=0,解得m=-8±
代入x2+(8-2m)x+m2-16=0,得m2+16m-64=0,解得m=-8±![]() (舍去负值).
(舍去负值).
综上所述,满足题设条件的m值应为m=0或-8+![]() .
.


科目:高中数学 来源: 题型:
| π | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| 3π |
| 2 |
| AC |
| BC |
| π |
| 2 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com