
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,已知cosC+(cosA﹣ ![]() sinA)cosB=0.
sinA)cosB=0.
(1)求角B的大小;
(2)若b= ![]() ,c=1,求△ABC的面积.
,c=1,求△ABC的面积.
【答案】
(1)解:在△ABC中,∵C=π﹣(A+B),cosC+(cosA﹣ ![]() sinA)cosB=0,
sinA)cosB=0,
∴﹣cos(A+B)+cosAcosB﹣ ![]() sinAcosB=0
sinAcosB=0
即sinAsinB﹣ ![]() sinAcosB=0
sinAcosB=0
∵sinA≠0,∴sinB﹣ ![]() cosB=0,即tanB=
cosB=0,即tanB= ![]() ,
,
∵0<B<π,∴ ![]()
(2)解:由余弦定理得,b2=a2+c2﹣2accosB,
把b= ![]() ,c=1代入得,3=a2+1﹣a,
,c=1代入得,3=a2+1﹣a,
即a2﹣a﹣2=0,解得a=2
∴ ![]()
【解析】(1)利用诱导公式、两角和的余弦公式、商的关系化简已知的式子,根据内角的范围和特殊角的三角函数值求出B的值;(2)由条件和余弦定理列出方程求出a的值,由三角形的面积公式求出△ABC的面积.
【考点精析】关于本题考查的正弦定理的定义和余弦定理的定义,需要了解正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() 才能得出正确答案.
才能得出正确答案.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+(1﹣a)x+(1﹣a).a∈R.
(1)当a=4时,解不等式f(x)≥7;
(2)若对P任意的x∈(﹣1,+∞),函数f(x)的图象恒在x轴上方,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆N经过点A(3,1),B(﹣1,3),且它的圆心在直线3x﹣y﹣2=0上.
(Ⅰ)求圆N的方程;
(Ⅱ)求圆N关于直线x﹣y+3=0对称的圆的方程.
(Ⅲ)若点D为圆N上任意一点,且点C(3,0),求线段CD的中点M的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直三棱柱ABC﹣A1B1C1中,若∠BAC=90°,AB=AC=AA1 , 则异面直线BA1与AC1所成的角等于( )
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx﹣x2 , a∈R,
(1)求函数f(x)的单调区间;
(2)若x≥1时,f(x)≤0恒成立,求实数a的取值范围;
(3)设a>0,若A(x1 , y1),B(x2 , y2)为曲线y=f(x)上的两个不同点,满足0<x1<x2 , 且x3∈
(x1 , x2),使得曲线y=f(x)在x=x3处的切线与直线AB平行,求证:x3< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2+Dx+Ey+3=0,圆C关于直线x+y﹣1=0对称,圆心在第二象限,半径为![]() .
.
(1)求圆C的方程;
(2)已知不过原点的直线l与圆C相切,且与x轴、y轴上的截距相等,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017黑龙江大庆实验中学仿真模拟】如图,在四棱锥P—ABCD中,平面PAD⊥底面ABCD,其中底面ABCD为等腰梯形,AD∥BC,PA=AB=BC=CD=2,PD=2![]() ,PA⊥PD,Q为PD的中点.
,PA⊥PD,Q为PD的中点.
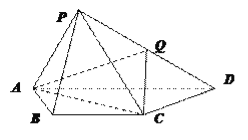
(Ⅰ)证明:CQ∥平面PAB;
(Ⅱ)求直线PD与平面AQC所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com