
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的值域;
的值域;
(2)若不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
(3)当![]() (
(![]() ,
, ![]() )时,函数
)时,函数![]() ,
, ![]() 的值域为
的值域为![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:
【题目】下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,均值与方差都不变;
②设有一个回归方程![]() ,变量x增加一个单位时,y平均增加3个单位;
,变量x增加一个单位时,y平均增加3个单位;
③线性回归方程![]() 必经过点
必经过点![]() ;
;
④在吸烟与患肺病这两个分类变量的计算中,从独立性检验知,有99%的把握认为吸烟与患肺病有关系时,我们说现有100人吸烟,那么其中有99人患肺病.其中错误的个数是( )
A. 0
B. 1
C. 2
D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在R上的奇函数,其中
是定义在R上的奇函数,其中![]() 为自然对数的底数.
为自然对数的底数.
(1)求实数![]() 的值;
的值;
(2)若存在![]() ,使得不等式
,使得不等式![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 在
在![]() 上不存在最值,求实数
上不存在最值,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知⊙C:x2+y2+2x-4y+1=0.
(1)若⊙C的切线在x轴、y轴上截距相等,求切线的方程.
(2)从圆外一点P(x0,y0)向圆引切线PM,M为切点,O为原点,若|PM|=|PO|,求使|PM|最小的P点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效的改良玉米品种,为农民提供技术支.现对已选出的一组玉米的茎高进行统计,获得茎叶图如右图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.
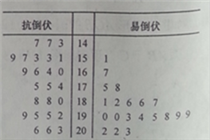 (1)完成列
(1)完成列![]() 联表,并判断是否可以在犯错误的概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关?
联表,并判断是否可以在犯错误的概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关?
(2)为了改良玉米品种,现采用分层抽样的方法从抗倒伏的玉米中抽出5株,再从这5株玉米中选取2株进行杂交试验,选取的植株均为矮茎的概率是多少?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:f(x)=2/(x-m)在区间(1,+∞)上是减函数;;命题q:2x-1+2m>0对任意x∈R恒成立.若(![]() p)∧q为真,求实数m的取值范围。
p)∧q为真,求实数m的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (m,n∈R)在x=1处取得极值2.
(m,n∈R)在x=1处取得极值2.
(1)求f(x)的解析式;
(2)k为何值时,方程f(x)-k=0只有1个根
(3)设函数g(x)=x2-2ax+a,若对于任意x1∈R,总存在x2∈[-1,0],使得g(x2)≤f(x1),求a的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() 为常数,
为常数,![]() ).(Ⅰ)求函数
).(Ⅰ)求函数![]() 的单调区间;(Ⅱ)当
的单调区间;(Ⅱ)当![]() 时,是否存在实数
时,是否存在实数![]() ,使得当
,使得当![]() 时,不等式
时,不等式![]() 恒成立?如果存在,求
恒成立?如果存在,求![]() 的取值范围;如果不存在,请说明理由(其中
的取值范围;如果不存在,请说明理由(其中![]() 是自然对数的底数,
是自然对数的底数,![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com